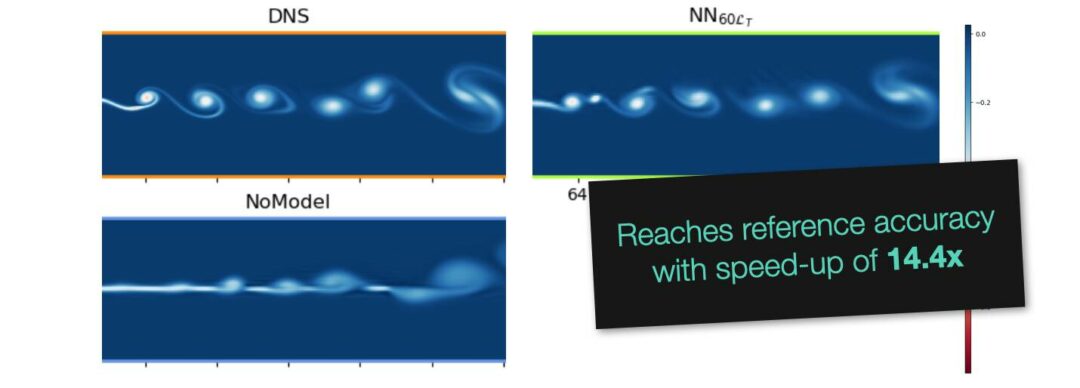
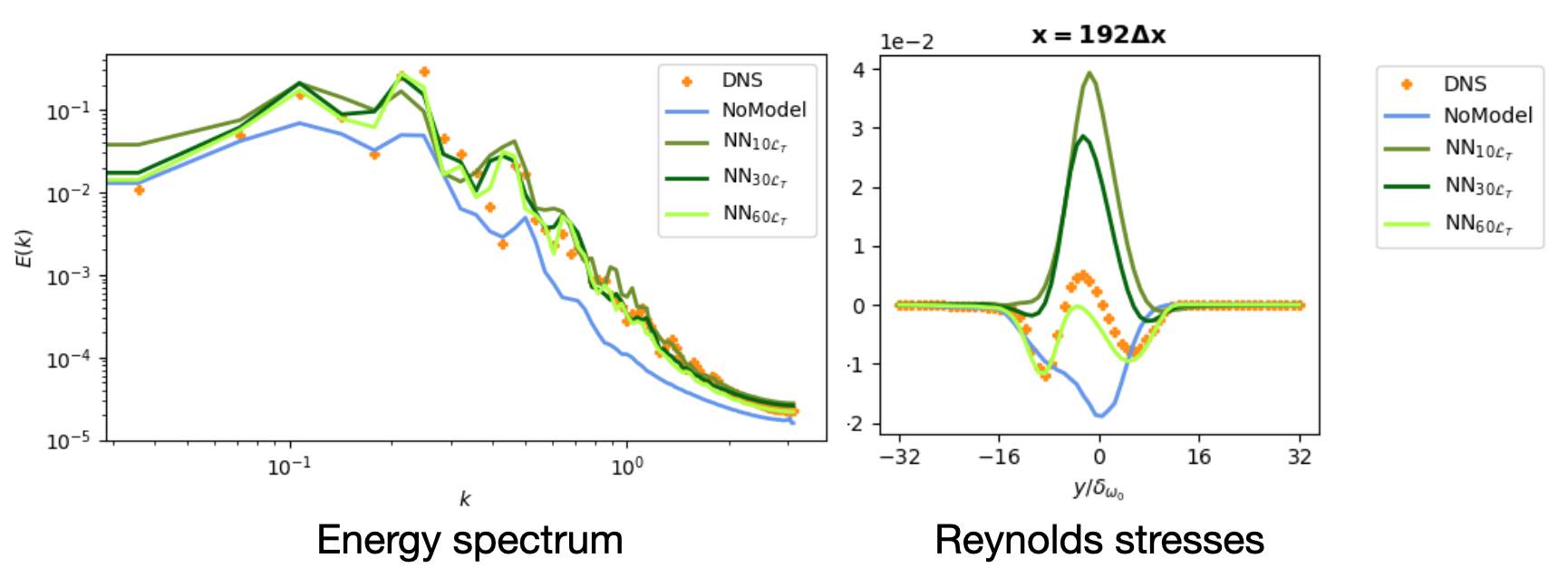
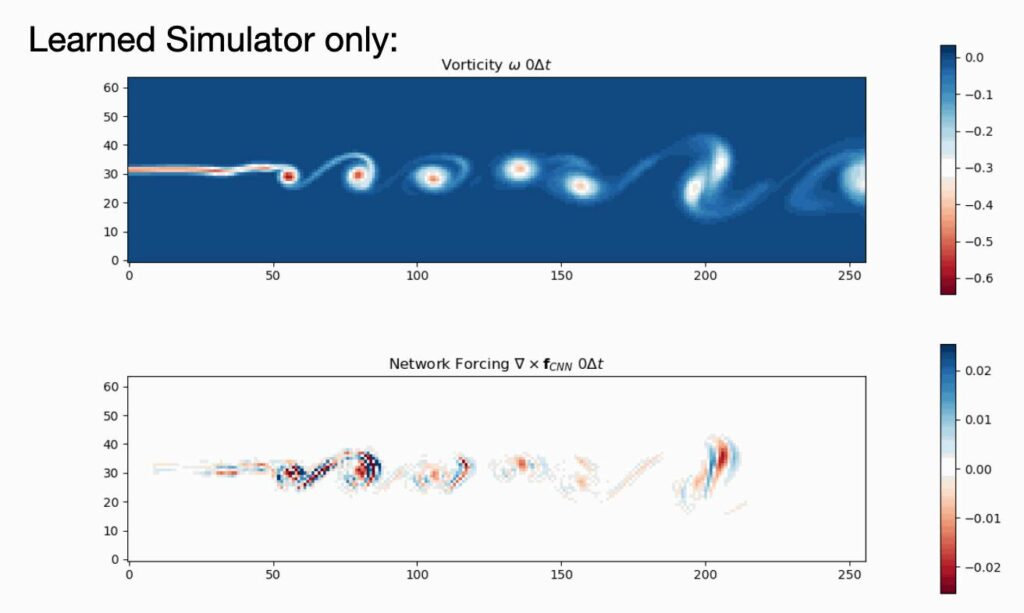
We’re happy to announce that our paper “Learning Similarity Metrics for Volumetric Simulations with Multiscale CNNs” was just accepted at the AAAI Conference on Artificial Intelligence.
It targets the similarity assessment of complex simulated datasets via an entropy-based CNN for 3D multi-channel data. The preprint can be found here https://arxiv.org/abs/2202.04109, or try it out yourself via a pretrained model at https://github.com/tum-pbs/VOLSIM.
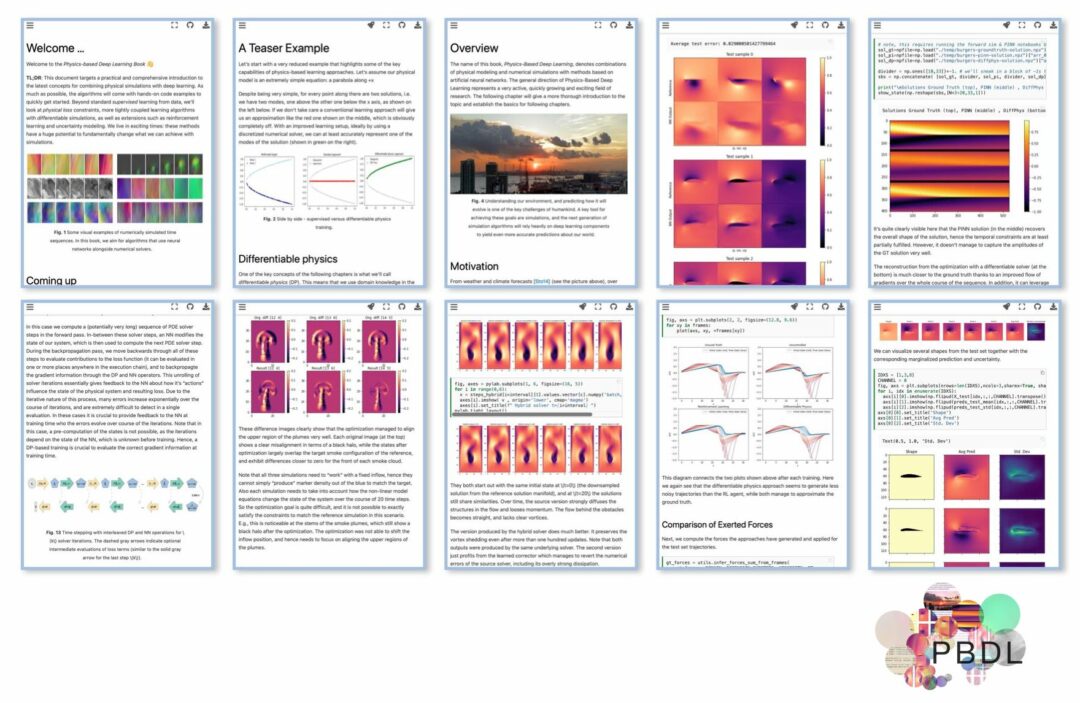
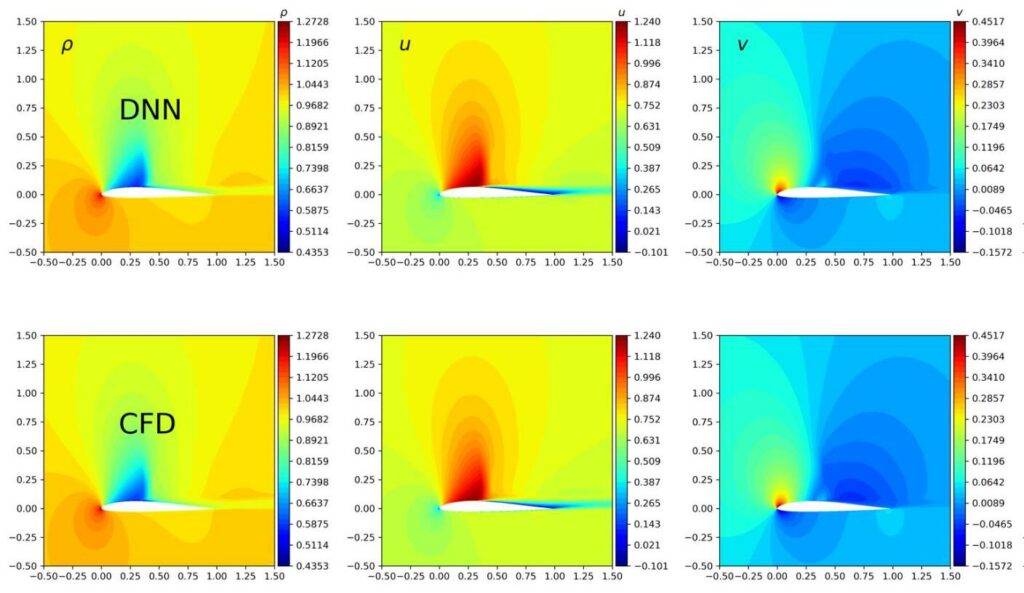
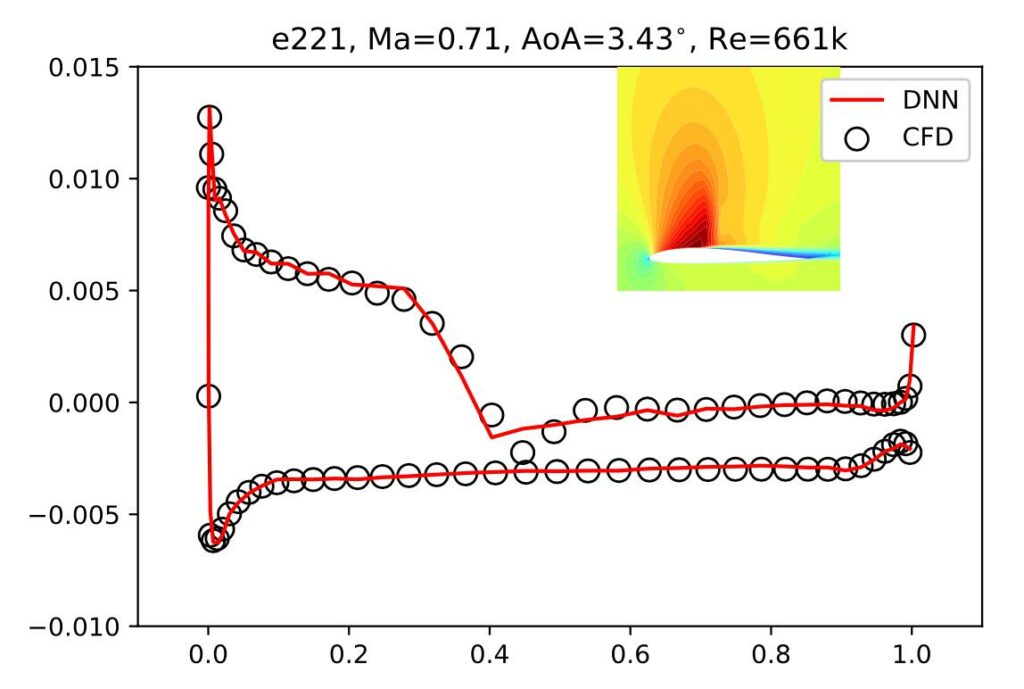
Full abstract: Simulations that produce three-dimensional data are ubiquitous in science, ranging from fluid flows to plasma physics. We propose a similarity model based on entropy, which allows for the creation of physically meaningful ground truth distances for the similarity assessment of scalar and vectorial data, produced from transport and motion-based simulations. Utilizing two data acquisition methods derived from this model, we create collections of fields from numerical PDE solvers and existing simulation data repositories, and highlight the importance of an appropriate data distribution for an effective training process. Furthermore, a multiscale CNN architecture that computes a volumetric similarity metric (VolSiM) is proposed. To the best of our knowledge this is the first learning method inherently designed to address the challenges arising for the similarity assessment of high-dimensional simulation data. Additionally, the tradeoff between a large batch size and an accurate correlation computation for correlation-based loss functions is investigated, and the metric’s invariance with respect to rotation and scale operations is analyzed. Finally, the robustness and generalization of VolSiM is evaluated on a large range of test data, as well as a particularly challenging turbulence case study, that is close to potential real-world applications.