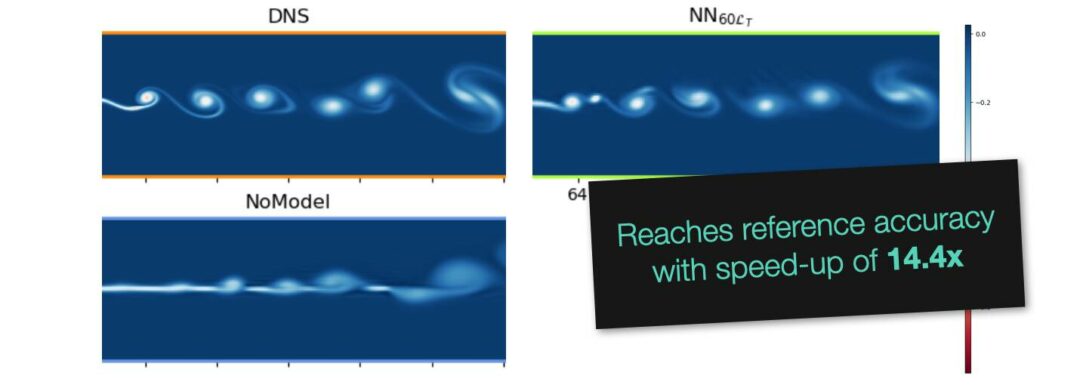
Below you can preview our newest paper on learned turbulence modeling with differentiable solvers. The learned model closely reproduces the turbulent statistics of the DNS reference, and matches it’s accuracy while being more than an order of magnitude faster. The training is performed jointly with a classic, second-order PISO solver that is made differentiable via phiflow.
Preprint available on arXiv: https://arxiv.org/abs/2202.06988
This is all based on a validated second-order-in-time PISO solver, that’s integrated into neural network training with the “differentiable physics” approach.

Abstract: In this paper, we train turbulence models based on convolutional neural networks. These learned turbulence models improve under-resolved low resolution solutions to the incompressible Navier-Stokes equations at simulation time. Our method involves the development of a differentiable numerical solver that supports the propagation of optimisation gradients through multiple solver steps. We showcase the significance of this property by demonstrating the superior stability and accuracy of those models that featured a higher number of unrolled steps during training. This approach is applied to three two-dimensional turbulence flow scenarios, a homogeneous decaying turbulence case, a temporally evolving mixing layer and a spatially evolving mixing layer. Our method achieves significant improvements of long-term a-posteriori statistics when compared to no-model simulations, without requiring these statistics to be directly included in the learning targets. At inference time, our proposed method also gains substantial performance improvements over similarly accurate, purely numerical methods.