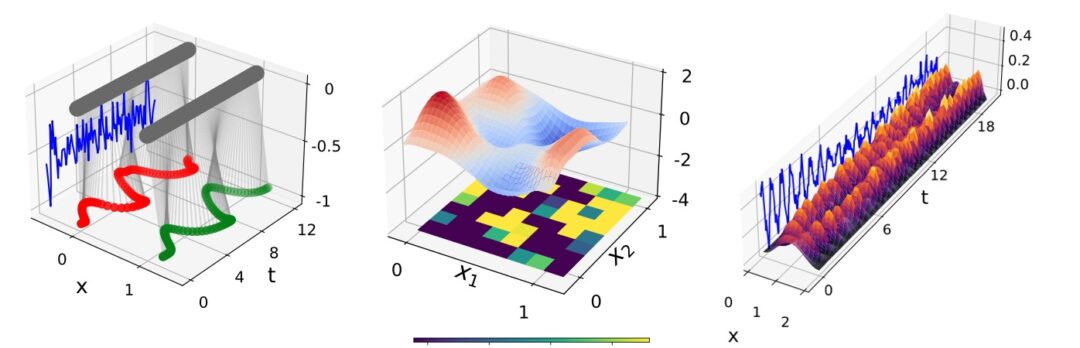
We’re happy to advertise our ICLR’22 spotlight paper on half-inverse gradients (HIGs) for physics problems in deep learning. We propose a new method that bridges the gap between “classical” optimizers and machine learning methods. We’re showing its advantages and behavior for a wide range of physical problems, from a simple non-linear oscillator, over a diffusion PDE, to a quantum dipole control problem. So – no Navier-Stokes, yet – but that’s definitely an exciting outlook 😀
arXiv preprint: https://arxiv.org/abs/2203.10131
Code repository: https://github.com/tum-pbs/half-inverse-gradients
Abstract: Recent works in deep learning have shown that integrating differentiable physics simulators into the training process can greatly improve the quality of results. Although this combination represents a more complex optimization task than supervised neural network training, the same gradient-based optimizers are typically employed to minimize the loss function. However, the integrated physics solvers have a profound effect on the gradient flow as manipulating scales in magnitude and direction is an inherent property of many physical processes. Consequently, the gradient flow is often highly unbalanced and creates an environment in which existing gradient-based optimizers perform poorly. In this work, we analyze the characteristics of both physical and neural network optimizations to derive a new method that does not suffer from this phenomenon. Our method is based on a half-inversion of the Jacobian and combines principles of both classical network and physics optimizers to solve the combined optimization task. Compared to state-of-the-art neural network optimizers, our method converges more quickly and yields better solutions, which we demonstrate on three complex learning problems involving nonlinear oscillators, the Schroedinger equation and the Poisson problem.