Thuerey Group

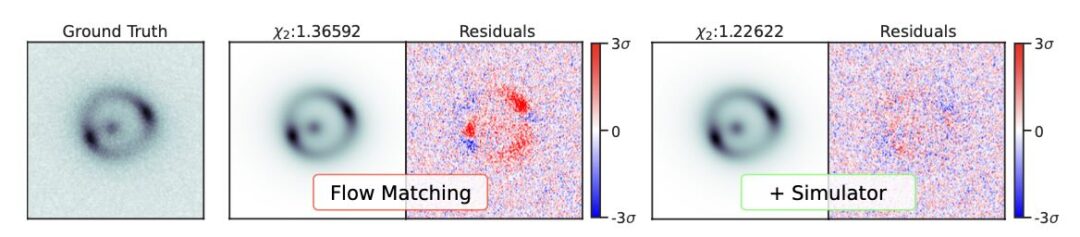
Our new NN architecture tailored to scientific tasks is online now, ready to be presented at ICML. It combines hierarchical processing (UDiT), scalability (SWin) and flexible conditioning mechanisms. Our ICML paper shows it outperforming existing SOTA architectures thanks to its custom combination of vision tricks. Code is up, everything ready to be presented in Vancouver by Benjamin soon 😁

Paper, code and tutorials are available at https://tum-pbs.github.io/pde-transformer/landing.html

Full abstract: We introduce PDE-Transformer, an improved transformer-based architecture for surrogate modeling of physics simulations on regular grids. We combine recent architectural improvements of diffusion transformers with adjustments specific for large-scale simulations to yield a more scalable and versatile general-purpose transformer architecture, which can be used as the backbone for building large-scale foundation models in physical sciences.
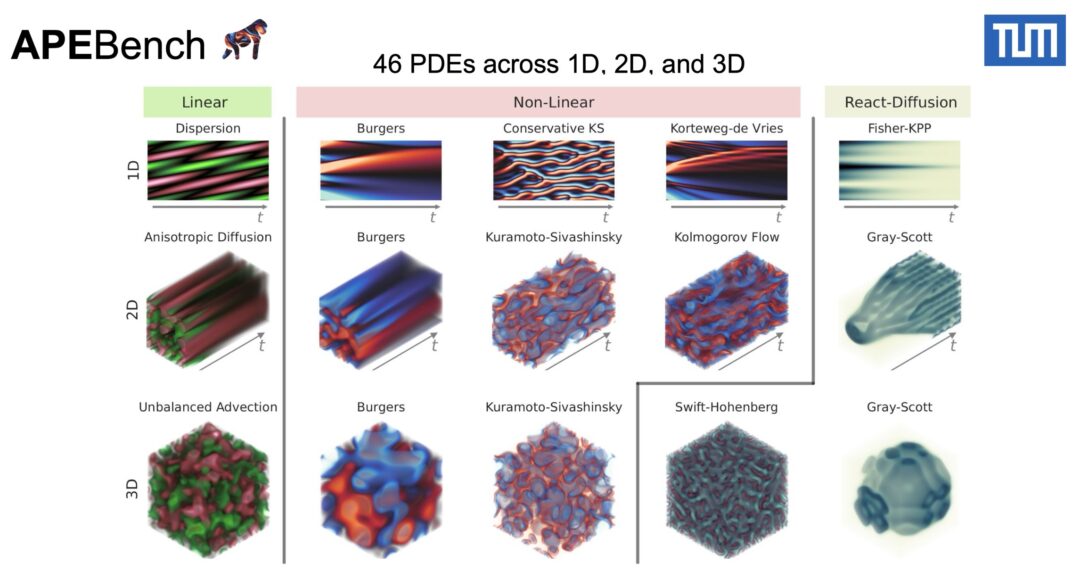
We demonstrate that our proposed architecture outperforms state-of-the-art transformer architectures for computer vision on a large dataset of 16 different types of PDEs. We propose to embed different physical channels individually as spatio-temporal tokens, which interact via channel-wise self-attention. This helps to maintain a consistent information density of tokens when learning multiple types of PDEs simultaneously.
Our pre-trained models achieve improved performance on several challenging downstream tasks compared to training from scratch and also beat other foundation model architectures for physics simulations.

We’re excited to share our latest work combining physics priors with probabilistic models: Flow Matching Meets PDEs – A Unified Framework for Physics-Constrained Generation , by Giacomo Baldan and Qiang Liu.

You can check out the full paper here! Central lessons learned are:

• Conflict-free updates are crucial for achieving very high physics-residual accuracies ✅
• Differentiable solvers can fundamentally enhance the distributional accuracy of the models ⭐️

Full paper abstract: Generative machine learning methods, such as diffusion models and flow matching, have shown great potential in modeling complex system behaviors and building efficient surrogate models. However, these methods typically learn the underlying physics implicitly from data. We propose Physics-Based Flow Matching (PBFM), a novel generative framework that explicitly embeds physical constraints, both PDE residuals and algebraic relations, into the flow matching objective. We also introduce temporal unrolling at training time that improves the accuracy of the final, noise-free sample prediction. Our method jointly minimizes the flow matching loss and the physics-based residual loss without requiring hyperparameter tuning of their relative weights. Additionally, we analyze the role of the minimum noise level, σmin, in the context of physical constraints and evaluate a stochastic sampling strategy that helps to reduce physical residuals. Through extensive benchmarks on three representative PDE problems, we show that our approach yields up to an 8× more accurate physical residuals compared to FM, while clearly outperforming existing algorithms in terms of distributional accuracy. PBFM thus provides a principled and efficient framework for surrogate modeling, uncertainty quantification, and accelerated simulation in physics and engineering applications.

While most numerical solvers focus on moving forward, sometimes you need to take a step back. Have you ever faced challenges like these?

• Solving Lagrangian inverse problems without an adjoint solver?
• Performing shape optimization, but your boundaries are non-differentiable?
• Building closure models when your SPH solver lacks gradients?

If you answered yes to any of these or similar questions, we’re excited to announce the first public release of Rene’s DiffSPH, our differentiable Smoothed Particle Hydrodynamics solver. DiffSPH can tackle all these challenges and more. It supports compressible, weakly-compressible, and incompressible fluids, all while being fully differentiable and written in PyTorch.

• Explore our repository: https://diffSPH.fluids.dev
• Check out a short live demo of a 1D Sod Shock Tube simulation in Colab

Our SIGGRAPH ’25 paper on super-large scale FLIP simulations with two-phases is online now. Bernhard’s solver is especially impressive given the fact that it’s all running on a single workstations, without GPU-support. The preview image above doesn’t do the simulations justice. Please enjoy the video in full-screen and high-quality via the link below:

• Video with additional Simulations
• Paper preprint
• MSBG Source-code

Full paper abstract: Capturing the visually compelling features of large-scale water phenomena,such as the spray clouds of crashing waves, stormy seas, or waterfalls, involves simulating not only the water but also the motion of the air interacting with it. However, current solutions in the visual effects industry still largely rely on single-phase solvers and non-physical “white-water” heuristics. To address these limitations, we present Phase-Field-FLIP (PF-FLIP), a hybrid Eulerian/Lagrangian method for the fully physics-based simulation of very large-scale, highly turbulent multiphase flows at high Reynolds numbers and high fluid density contrasts. PF-FLIP transports mass and momentum in a consistent, non-dissipative manner and, unlike most existing multiphase approaches, does not require a surface reconstruction step. Furthermore, we employ spatial adaptivity across all critical components of the simulation algorithm, including the pressure Poisson solver. We augment PF-FLIP with a dual multiresolution scheme that couples an efficient treeless adaptive grid with adaptive particles, along with a fast adaptive Poisson solver tailored for high-density-contrast multiphase flows. Our method enables the simulation of two-phase flow scenarios with a level of physical realism and detail previously unattainable in graphics, supporting billions of particles and adaptive 3D resolutions with thousands of grid cells per dimension on a single workstation.

We are releasing our PICT solver! 🥳 it features a fully-differentiable, accurate and validated incompressible Navier-Stokes solver with seamless PyTorch integration. This enables a wide variety of neat learning tasks, such as correcting Neural operators, closure learning and inverse problems. You can find a first few examples in the accompanying paper below. Please give it a try, and let us know how it works 🤔🙏

• Source Code: https://github.com/tum-pbs/PICT
• Paper with Examples: https://arxiv.org/abs/2505.16992
• Overview Video: https://youtu.be/GGLidL0oT3s

Key results and properties of the solver are
✅ Accurate and optimized gradients
✅ Handles 2D & 3D turbulence cases
✅ Learn sub-grid scale (SGS) models from statistics alone
✅ Verified on classic benchmarks
✅ Runs faster than high-fidelty simulations — with comparable (or even better) accuracy

The following computational graph gives an overview of the approach. A key distinguishing feature of PICT are its tailored and efficient gradient calculations that can be leveraged to substantially accelerate back-propagation to facilitate learning tasks. E.g., the implicit derivative operators can be used deactivate parts of the backwards task in early learning stages, and enable them later on for “fine-tuning”.

Full paper abstract: Despite decades of advancements, the simulation of fluids remains one of the most challenging areas of in scientific computing. Supported by the necessity of gradient information in deep learning, differentiable simulators have emerged as an effective tool for optimization and learning in physics simulations. In this work, we present our fluid simulator PICT, a differentiable pressure-implicit solver coded in PyTorch with Graphics-processing-unit (GPU) support. We first verify the accuracy of both the forward simulation and our derived gradients in various established benchmarks like lid-driven cavities and turbulent channel flows before we show that the gradients provided by our solver can be used to learn complicated turbulence models in 2D and 3D. We apply both supervised and unsupervised training regimes using physical priors to match flow statistics. In particular, we learn a stable sub-grid scale (SGS) model for a 3D turbulent channel flow purely based on reference statistics. The low-resolution corrector trained with our solver runs substantially faster than the highly resolved references, while keeping or even surpassing their accuracy. Finally, we give additional insights into the physical interpretation of different solver gradients, and motivate a physically informed regularization technique.

I wanted to highlight PBDL’s brand-new sections on diffusion models with code and derivations! Great work by Benjamin Holzschuh, with neat Jupyter notebooks 👍 It covers all the “generative AI” basics, from normalizing flow basics over score matching to denoising & flow matching.

Here are a few examples to check out:

• Normalizing flows: https://colab.research.google.com/github/tum-pbs/pbdl-book/blob/master/probmodels-normflow.ipynb
• Flow matching: https://colab.research.google.com/github/tum-pbs/pbdl-book/blob/master/probmodels-flowmatching.ipynb

Feel free to give it a try 😀 , and let us know whether it’s understandable / works / where to improve…

For everyone visiting ICLR 2025 in Singapore, please check out one of our oral talks / spotlights / posters 😀

• Learning Distributions of Complex Fluid Simulations with Diffusion Graph Networks , https://openreview.net/forum?id=uKZdlihDDn
• ConFIG: Towards Conflict-free Training of Physics Informed Neural Networks , https://openreview.net/forum?id=APojAzJQiq
• Progressively Refined Differentiable Physics , https://openreview.net/forum?id=9Fh0z1JmPU
• Truncation Is All You Need: Improved Sampling Of Diffusion Models For Physics-Based Simulations , https://openreview.net/forum?id=0FbzC7B9xI
• Temporal Difference Learning: Why It Can Be Fast and How It Will Be Faster , https://openreview.net/forum?id=j3bKnEidtT

We’re excited to highlight PBDL v0.3 at https://www.physicsbaseddeeplearning.org/, the latest version of our physics-based deep learning “book”. This version features a huge new chapter on generative AI, covering topics ranging from the derivation, over graph-based inference to physics-based constraints… Thanks to all those who contributed to this version, especially: Benjamin, Georg, Mario and Qiang!

The full PDF version can be found at: http://arxiv.org/pdf/2109.05237

Synopsis: PBDL is a hands-on, comprehensive guide to deep learning in the realm of physical simulations. Rather than just theory, we emphasize practical application: every concept is paired with interactive Jupyter notebooks to get you up and running quickly. Beyond traditional supervised learning, we dive into physical loss-constraints, differentiable simulations, diffusion-based approaches for probabilistic generative AI, as well as reinforcement learning and advanced neural network architectures. These foundations are paving the way for the next generation of scientific foundation models. We are living in an era of rapid transformation. These methods have the potential to redefine what’s possible in computational science.

As a sneak preview, the next chapters will show:

• How to train neural networks to predict the fluid flow around airfoils with diffusion modeling. This gives a probabilistic surrogate model that replaces and outperforms traditional simulators.
• How to use model equations as residuals to train networks that represent solutions, and how to improve upon these residual constraints by using differentiable simulations.
• How to more tightly interact with a full simulator for inverse problems. E.g., we’ll demonstrate how to circumvent the convergence problems of standard reinforcement learning techniques by leveraging simulators in the training loop.
• We’ll also discuss the importance of choosing the right network architecture: whether to consider global or local interactions, continuous or discrete representations, and structured versus unstructured graph meshes.

Congratulations to Kanishk and Felix 👍 for their #ICLR’25 paper “Progressively Refined Differentiable Physics” https://kanishkbh.github.io/prdp-paper/ , the key insight is that training can be accelerated substantially by using fast approximates of the gradient (especially in early phases of training).

Full paper abstract: The physics solvers employed for neural network training are primarily iterative, and hence, differentiating through them introduces a severe computational burden as iterations grow large. Inspired by works in bilevel optimization, we show that full accuracy of the network is achievable through physics significantly coarser than fully converged solvers. We propose progressively refined differentiable physics (PRDP), an approach that identifies the level of physics refinement sufficient for full training accuracy. By beginning with coarse physics, adaptively refining it during training, and stopping refinement at the level adequate for training, it enables significant compute savings without sacrificing network accuracy. Our focus is on differentiating iterative linear solvers for sparsely discretized differential operators, which are fundamental to scientific computing. PRDP is applicable to both unrolled and implicit differentiation. We validate its performance on a variety of learning scenarios involving differentiable physics solvers such as inverse problems, autoregressive neural emulators, and correction-based neural-hybrid solvers. In the challenging example of emulating the Navier-Stokes equations, we reduce training time by 62%.

Congratulations to Youssef and Benjamin 👍 for their ICLR 2025 paper on Truncated Diffusion Sampling. It investigates several key questions of generative AI and diffusion for physics simulations to improve accuracy via Tweedie’s formula.

Improved Sampling of Diffusion Models in Fluid Dynamics with Tweedie’s Formula (originally titled “Truncation Is All You Need: Improved Sampling Of Diffusion Models For Physics-Based Simulations”)

Full abstract: State-of-the-art Denoising Diffusion Probabilistic Models (DDPMs) rely on an expensive sampling process with a large Number of Function Evaluations (NFEs) to provide high-fidelity predictions. This computational bottleneck renders diffusion models less appealing as surrogates for the spatio-temporal prediction of physics-based problems with long rollout horizons. We propose Truncated Sampling Models, enabling single-step and few-step sampling with elevated fidelity by simple truncation of the diffusion process, reducing the gap between DDPMs and deterministic single-step approaches. We also introduce a novel approach, Iterative Refinement, to sample pre-trained DDPMs by reformulating the generative process as a refinement process with few sampling steps. Both proposed methods enable significant improvements in accuracy compared to DDPMs, DDIMs, and EDMs with NFEs ≤10 on a diverse set of experiments, including incompressible and compressible turbulent flow and airfoil flow uncertainty simulations. Our proposed methods provide stable predictions for long rollout horizons in time-dependent problems and are able to learn all modes of the data distribution in steady-state problems with high uncertainty.

Great to see APEBench (our work from NeurIPS’24) featured on the MCML blog: “Can AI Help Solve Complex Physics Equations? Meet APEBench, an innovative benchmark suite introduced by our Junior Member Felix Köhler, together with our PIs Rüdiger Westermann and Nils Thuerey as well as co-author Simon Niedermayr.”

The full text can be found here

In this paper we solve the decades-old puzzle of why temporal difference learning (TD) can solve complex reinforcement learning (RL) tasks that Gradient Descent cannot. Our novel theoretical view shows how TD (in 2D) effectively counters ill-conditioning, the very property that makes gradient methods impractically slow. This has the potential to become a cornerstone theorem in modern optimization, suggesting that the future for unsupervised, physics-informed deep learning lies in “non-gradient” methods.

Full paper: https://openreview.net/forum?id=j3bKnEidtT

Full abstract: Temporal difference (TD) learning represents a fascinating paradox: It is the prime example of a divergent algorithm that has not vanished after its instability was proven. On the contrary, TD continues to thrive in reinforcement learning (RL), suggesting that it provides significant compensatory benefits. Empirical evidence supports this, as many RL tasks require substantial computational resources, and TD delivers a crucial speed advantage that makes these tasks solvable. However, it is limited to cases where the divergence issues are absent or negligible for unknown reasons. So far, the theoretical foundations behind the speed-up are also unclear. In our work, we address these shortcomings of TD by employing techniques for analyzing iterative schemes developed over the past century. Our analysis reveals that TD possesses a mechanism enabling efficient mapping into the smallest eigenspace—an operation previously thought to necessitate costly matrix inversion. Notably, this effect is independent of the conditioning of the problem, making it particularly well-suited for RL tasks characterized by rapidly increasing condition numbers through delayed rewards. Our novel theoretical understanding allows us to develop a scalable algorithm that integrates TD’s speed with the reliable convergence of gradient descent (GD). We additionally validate these improvements through a rigorous mathematical proof in two dimensions, as well as experiments on problems where TD and GD falter, providing valuable insights into the future of optimization techniques in artificial intelligence.

A second ICLR paper is our ConFIG paper, which has been online for a while now (Congrats to Qiang 👏). The ConFIG method is a generic method for optimization problems involving multiple loss terms (e.g., Multi-task Learning, Continuous Learning, and Physics Informed Neural Networks). It prevents the optimization from getting stuck into a local minimum of a specific loss term due to the conflict between losses. On the contrary, it leads the optimization to the shared minimum of all losses by providing a conflict-free update direction.

Source code and examples available in this GitHub repo.

Full abstract: The loss functions of many learning problems contain multiple additive terms that can disagree and yield conflicting update directions. For Physics-Informed Neural Networks (PINNs), loss terms on initial/boundary conditions and physics equations are particularly interesting as they are well-established as highly difficult tasks. To improve learning the challenging multi-objective task posed by PINNs, we propose the ConFIG method, which provides conflict-free updates by ensuring a positive dot product between the final update and each loss-specific gradient. It also maintains consistent optimization rates for all loss terms and dynamically adjusts gradient magnitudes based on conflict levels. We additionally leverage momentum to accelerate optimizations by alternating the back-propagation of different loss terms. The proposed method is evaluated across a range of challenging PINN scenarios, consistently showing superior performance and runtime compared to baseline methods. We also test the proposed method in a classic multi-task benchmark, where the ConFIG method likewise exhibits a highly promising performance.

We’d like to highlight a first one of our this year’s ICLR papers: “Diffusion Graph Nets” (Congrats to Mario 👏 ). The paper targets predicting complex distributions of flow states on unstructured meshes (https://openreview.net/forum?id=uKZdlihDDn). It’s not only highly efficient, but also excels at “completing” distributions: it works even if the training data contains only a fraction of the flow statistics per case. Above are some examples for turbulent flows in 3D over a wing.

It’s also worth mentioning that the code is already online at https://github.com/tum-pbs/dgn4cfd , complete with notebooks, flow matching, and the full hierarchical diffusion graph net architecture. If you’re trying it, please let us know how it works for you!

Full abstract: Physical systems with complex unsteady dynamics, such as fluid flows, are often poorly represented by a single mean solution. For many practical applications, it is crucial to access the full distribution of possible states, from which relevant statistics (e.g., RMS and two-point correlations) can be derived. Here, we propose a graph-based latent diffusion model that enables direct sampling of states from their equilibrium distribution, given a mesh discretization of the system and its physical parameters. This allows for the efficient computation of flow statistics without running long and expensive numerical simulations. The graph-based structure enables operations on unstructured meshes, which is critical for representing complex geometries with spatially localized high gradients, while latent-space diffusion modeling with a multi-scale GNN allows for efficient learning and inference of entire distributions of solutions. A key finding of our work is that the proposed networks can accurately learn full distributions even when trained on incomplete data from relatively short simulations. We apply this method to a range of fluid dynamics tasks, such as predicting pressure distributions on 3D wing models in turbulent flow, demonstrating both accuracy and computational efficiency in challenging scenarios. The ability to directly sample accurate solutions, and capturing their diversity from short ground-truth simulations, is highly promising for complex scientific modeling tasks.

Thanks to everyone contributing to our five accepted ICLR papers for the hard work! Great job Mario, Tobias, Qiang, Rachel, Kanishk, Felix, Youssef, Benjamin, Patrick, and Luca 👍 Here’s a quick list, stay tuned for details & code in the upcoming weeks:

• Learning Distributions of Complex Fluid Simulations with Diffusion Graph Networks , https://openreview.net/forum?id=uKZdlihDDn
• ConFIG: Towards Conflict-free Training of Physics Informed Neural Networks , https://openreview.net/forum?id=APojAzJQiq
• Progressively Refined Differentiable Physics , https://openreview.net/forum?id=9Fh0z1JmPU
• Truncation Is All You Need: Improved Sampling Of Diffusion Models For Physics-Based Simulations , https://openreview.net/forum?id=0FbzC7B9xI
• Temporal Difference Learning: Why It Can Be Fast and How It Will Be Faster , https://openreview.net/forum?id=j3bKnEidtT

It is also worth highlightig our new PBDL dataloader project: https://github.com/tum-pbs/pbdl-dataset, created by TUM Bachelor student Sebastian Pfister. It provides convenient access to our datasets.

Our “classic” airfoil learning example using the loader can be found under the link below. It is very concise now: https://colab.research.google.com/github/tum-pbs/pbdl-book/blob/master/supervised-airfoils.ipynb

The current content is:

• Incompressible Navier-Stokes wake flow over time
• Transonic (compressible) cylinder flow
• A simple NS wake flow (Solver-in-the-Loop)
• Kuramoto-Sivashinsky in 1D (chaotic)
• and a Reynolds-averaged airfoil flow data set.

More datasets to come in the next weeks! 😀

I’m excited to share our APEBench paper and the corresponding source code, to be presented at NeurIPS. Congratulations Felix and Simon 😀 👍 At its core, APEBench features a lightning-fast ⚡️ fully differentiable spectral solver with a huge range of differen PDEs.

• Paper http://arxiv.org/abs/2411.00180
• Source code https://github.com/tum-pbs/apebench

It also comes with an integrated GPU-based volume renderer “VAPE” (https://keksboter.github.io/vape4d/), that works in your browser (and in Jupyter). If you’re patient, try it here (note – this link downloads 100MB, so it can take a moment): https://vape.niedermayr.dev/?file=https://huggingface.co/datasets/vollautomat/vape4d/resolve/main/gray_scott_3d.npy&colormap=https://huggingface.co/datasets/vollautomat/vape4d/resolve/main/colormap.json

Paper abstract: We introduce the Autoregressive PDE Emulator Benchmark (APEBench), a comprehensive benchmark suite to evaluate autoregressive neural emulators for solving partial differential equations. APEBench is based on JAX and provides a seamlessly integrated differentiable simulation framework employing efficient pseudo-spectral methods, enabling 46 distinct PDEs across 1D, 2D, and 3D. Facilitating systematic analysis and comparison of learned emulators, we propose a novel taxonomy for unrolled training and introduce a unique identifier for PDE dynamics that directly relates to the stability criteria of classical numerical methods. APEBench enables the evaluation of diverse neural architectures, and unlike existing benchmarks, its tight integration of the solver enables support for differentiable physics training and neural-hybrid emulators. Moreover, APEBench emphasizes rollout metrics to understand temporal generalization, providing insights into the long-term behavior of emulating PDE dynamics. In several experiments, we highlight the similarities between neural emulators and numerical simulators.

Our paper “Flow Matching for Posterior Inference with Simulator Feedback” is available on arXiv now: https://arxiv.org/abs/2410.22573 The key idea is to incorporate physics-constraints with guiding so that the posterior isn’t becoming biased… This gives highly accurate solutions, better than pure learning!

Code will be available at https://github.com/tum-pbs/sbi-sim

Full abstract:
Flow-based generative modeling is a powerful tool for solving inverse
problems in physical sciences that can be used for sampling and likelihood
evaluation with much lower inference times than traditional methods. We propose
to refine flows with additional control signals based on a simulator. Control
signals can include gradients and a problem-specific cost function if the
simulator is differentiable, or they can be fully learned from the simulator
output. In our proposed method, we pretrain the flow network and include
feedback from the simulator exclusively for finetuning, therefore requiring
only a small amount of additional parameters and compute. We motivate our
design choices on several benchmark problems for simulation-based inference and
evaluate flow matching with simulator feedback against classical MCMC methods
for modeling strong gravitational lens systems, a challenging inverse problem
in astronomy. We demonstrate that including feedback from the simulator
improves the accuracy by 53%, making it competitive with traditional
techniques while being up to 67x faster for inference.

Our paper on training recurrent Neural operators with a solver-in-the-loop was now finally officially accepted at CMAME! Congratulations Bjoern 😀 👍 In parallel, we’ve been updating the paper https://arxiv.org/pdf/2402.12971 and the source code https://github.com/tum-pbs/unrolling Feel free to give it a try, and let us know how it works!

We actually have to thank the anonymous CMAME reviewers 🙏 They’ve successfully motivated us to substantially update the submission, which resulted in a big update of the paper. The theory was clarified, we included a 3D case, and with all the results being redone with relative errors the improvements are actually more substantial: moving from pure prediction to correction with unrolling yields more than 10x improvement for identical NNs.

Here’s the official CMAME link: https://authors.elsevier.com/sd/article/S0045-7825(24)00696-0