Authors: Nils Thuerey, K. Weissenow, L. Prantl, Xiangyu Hu
Abstract: We investigate the accuracy of deep learning models for the inference of Reynolds-Averaged Navier-Stokes turbulence simulations. We focus on a modernized U-net architecture, and evaluate a large number of trained neural networks with respect to their accuracy for the calculation of pressure and velocity fields. In particular, we illustrate how training data size and the number of weights in the networks interact. With our best models we arrive at a mean relative pressure and velocity error of less than 3% across a range of previously unseen airfoil shapes. In addition all source code is publicly available in order to ensure reproducibility and to provide a starting point for researchers interested in deep learning methods for physics problems. While this work focuses on RANS solutions, the neural network architecture and learning setup are very generic, and applicable to a wide range of PDE problems with field data.
Links![]() Preprint (arXiv)
Preprint (arXiv)![]() AIAA Journal
AIAA Journal![]() Code & Data
Code & Data
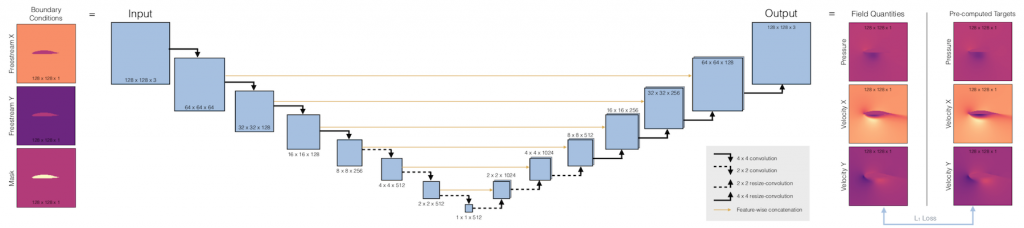
Fig. 1: Overview of the network architecture (a U-net) and the input / output data.
Introduction: Despite the enormous success of deep learning methods in the field of computer vision [KSH12, IZZE16, KALL17], and first success stories of applications in the area of physics simu- lations [TSSP16, XFCT18, BFM18, RYK18, BSHHB18], the corrsponding research communities retain a skeptical stance towards deep learning algorithms [Dur18]. This skepticism is often driven by concerns about the accuracy achievable with deep learning approaches. The advances of practical deep learning algorithms have significantly outpaced the under- lying theory [YSJ18], and hence many researchers see these methods as black-box methods that cannot be understood or analyzed.
With the following study our goal is to investigate the accuracy of trained deep learning models in order to alleviate some of these concerns. We also illustrate that despite the lack of proofs, deep learning methods can be analyzed and employed thanks to the large number of existing practical examples. We show how the accuracy of flow predictions around airfoil shapes changes with respect to the central training parameters, namely network size, and the number of training data samples. Additionally, we will demonstrate that the trained models yield a very high computational performance ”out-of-the-box”.
A second closely connected goal of our work is to provide a public test bed and evaluation platform for deep learning methods in the context of computational fluid dynamics (CFD). Both code and training data are publicly available at https://github.com/thunil/Deep-Flow-Prediction [TMM+18], and are kept as simple as possible to allow for quick adoption for experiments and further studies. As learning task we focus on the inference of Eulerian field functions, more specifically solutions of flow problems on Cartesian grids in terms of velocity and pressure distributions. Deep learning as a tool makes sense in this setting, as the functions were are interested in, i.e. velocity and pressure, are well represented on Cartesian grids, and convolutional layers, as a particularly powerful component of current deep learning methods, are especially well suited for such grids.
The learning task for our goal is very simple when seen on a high level: given enough training data, we have a unique relationship between boundary conditions and solution, we have full control of the data generation process, very little noise in the solutions, and we can train our models in a fully supervised manner. The difficulties rather stem from the non-linearities of the solutions, and the high requirements for accuracy. To illustrate the inherent capabilities of deep learning in the context of flow simulations we will also in- tentionally refrain from including any specialized physical priors such as conservation laws. Instead, we will employ straightforward, state-of-the-art convolutional neural network (CNN) architectures and evaluate in detail, based on more than 500 trained CNN models, how well they can capture the non-linear behavior of the Reynolds-averaged Navier-Stokes (RANS) equations. As a consequence, the setup we describe in the following is a very generic approach for PDE boundary value problems, and as such is applicable to a variety of other equations beyond RANS.
Acknowledgements: we thank H. Mehrotra and N. Mainali for their help with initial tests.

