ICLR 2020; arXiv, 1907.05279

Authors
Lukas Prantl, Technical University of Munich
Nuttapong Chentanez, NVIDIA
Stefan Jeschke, NVIDIA
Nils Thuerey, Technical University of Munich

Abstract
Point clouds, as a form of Lagrangian representation, allow for powerful and flexible applications in a large number of computational disciplines. We propose a novel deep-learning method to learn stable and temporally coherent feature spaces for points clouds that change over time. We identify a set of inherent problems with these approaches: without knowledge of the time dimension, the inferred solutions can exhibit strong flickering, and easy solutions to suppress this flickering can result in undesirable local minima that manifest themselves as halo structures. We propose a novel temporal loss function that takes into account higher time derivatives of the point positions, and encourages mingling, i.e., to prevent the aforementioned halos. We combine these techniques in a super-resolution method with a truncation approach to flexibly adapt the size of the generated positions. We show that our method works for large, deforming point sets from different sources to demonstrate the flexibility of our approach.

Links
OpenReview
arXiv preprint
Video
Source Code
Website

Further Information
Deep learning methods have proven themselves as powerful computational tools in many disciplines, and within it a topic of strongly growing interest is deep learning for point-based data sets. These Lagrangian representations are challenging for learning methods due to their unordered nature, but are highly useful in a variety of settings from geometry processing and 3D scanning to physical simulations, and since the seminal work of Qi Charles et al. (2017), a range of powerful inference tasks can be achieved based on point sets. Despite their success, interestingly, no works so far have taken into account time. Our world, and the objects within it, naturally move and change over time, and as such it is crucial for flexible point-based inference to take the time dimension into account.
In our work we mainly consider three dimensional data with a very high particle count, which can lead to considerable memory problems. An additional challenge is to deal with varying input sizes, and for super-resolution tasks, also varying output sizes. Thus, in summary we target an extremely challenging learning problem: we are facing permutation-invariant inputs and targets of varying size, that dynamically move and deform over time.

In this context, we propose a method to learn temporally stable representations for point-based data sets, and demonstrate its usefulness in the context of super-resolution. In order to enable deep learning approaches in this context, we make the following key contributions:

  • Dynamic local upsampling by dividing  a data set into small patches.
  • Permutation invariant loss terms for temporally coherent point set generation.
  • A Siamese training setup and generator architecture for point-based super-resolution with neural networks.
  • Enabling improved output variance by allowing for dynamic adjustments of the output size.
  • The identification of a specialized form of mode collapse for temporal point networks, together with a loss term to remove them.

We demonstrate that these contributions together make it possible to infer stable solutions for dynamically moving point clouds with millions of points.

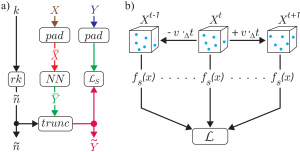Fig. 1: a) Schematic overview of our approach.  b) Siamese network setup for temporal loss calculation.
X … input data with k points
Y … ground-truth data with n points
Ỹ … generated data wit ñ points