Solver-in-the-Loop: Learning from Differentiable Physics to Interact with Iterative PDE-Solvers

Advances in Neural Information Processing (NeurIPS)
Authors  Kiwon Um, Raymond Fei, Robert Brand, Philipp Holl, Nils Thuerey

Abstract

Finding accurate solutions to partial differential equations (PDEs) is a crucial task in all scientific and engineering disciplines. It has recently been shown that machine learning methods can improve the solution accuracy by correcting for effects not captured by the discretized PDE. We target the problem of reducing numerical errors of iterative PDE solvers and compare different learning approaches for finding complex correction functions. We find that previously used learning approaches are significantly outperformed by methods that integrate the solver into the training loop and thereby allow the model to interact with the PDE during training. This provides the model with realistic input distributions that take previous corrections into account, yielding improvements in accuracy with stable rollouts of several hundred recurrent evaluation steps and surpassing even tailored supervised variants. We highlight the performance of the differentiable physics networks for a wide variety of PDEs, from non-linear advection-diffusion systems to three-dimensional Navier-Stokes flows.

Links
Preprint
NeurIPS 2020 Version
Code
Video with Supplemental Results
Overview Talk

---

Numerical methods are prevalent in science to improve the understanding of our world, with applications ranging from climate modeling over simulating the efficiency of airplane wings to analyzing blood flow in a human body. These applications are extremely costly to compute due to the fine spatial and temporal resolutions required in real-world scenarios. In this context, deep learning methods are receiving strongly growing attention and show promise to account for those components of the solutions that are difficult to resolve or are not well captured by our physical models. Physical models typically come in the form of PDEs and are discretized in order to be processed by computers. This step inevitably introduces numerical errors. Despite a vast amount of work and experimental evaluations, analytic descriptions of these errors remain elusive for most real-world applications of simulations.

In our work, we specifically target the numerical errors that arise in the discretization of PDEs. We show that, despite the lack of closed-form descriptions, discretization errors can be seen as functions with regular and repeating structures and, thus, can be learned by neural networks. Once trained, such a network can be evaluated locally to improve the solution of a PDE-solver, i.e., to reduce its numerical error.

The core of most numerical methods contains some form of iterative process – either in the form of repeated updates over time for explicit solvers or even within a single update step for implicit solvers. Hence, we focus on iterative PDE solving algorithms. We show that neural networks can only achieve optimal performance if they take the reaction of the solver into account. This interaction is not possible with supervised learning on pre-computed data alone. Even small inference errors of a supervised model can quickly accumulate over time, leading to a data distribution that differs from the distribution of the pre-computed data. For supervised learning methods, this causes deteriorated inference at best and solver explosions at worst.

We demonstrate that neural networks can be successfully trained if they can interact with the respective PDE solver during training. To achieve this, we leverage differentiable simulations. Differentiable simulations allow a trained model to autonomously explore and experience the physical environment and receive directed feedback regarding its interactions throughout the solver iterations. Hence, our work fits into the broader context of machine learning as differentiable programming, and we specifically target recurrent interactions of highly non-linear PDEs with deep neural networks. This combination bears particular promise: it improves generalizing capabilities of the trained models by letting the PDE-solver handle large-scale changes to the data distribution such that the learned model can focus on localized structures not captured by the discretization. While physical models generalize very well, learned models often specialize in data distributions seen at training time. However, we will show that, by combining PDE-based solvers with a learned model, we can arrive at hybrid methods that yield improved accuracy while handling solution manifolds with significant amounts of varying physical behavior.

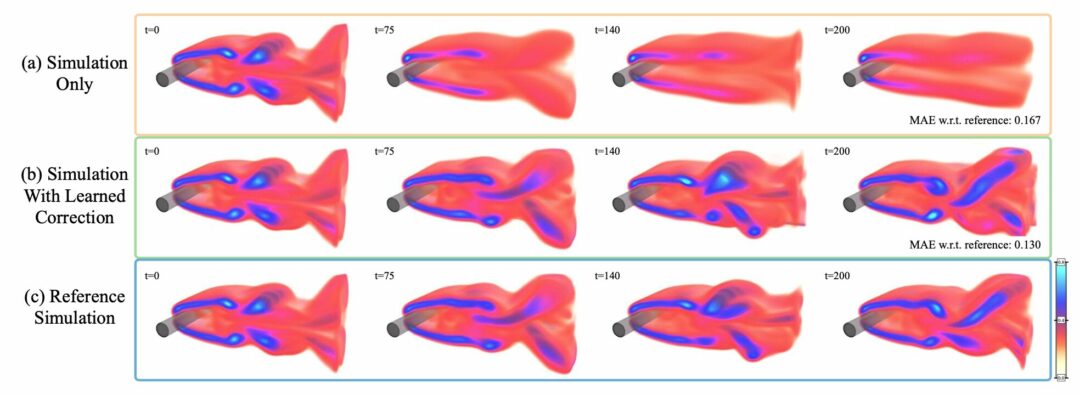
We show the advantages of training via differentiable physics for explicit and implicit solvers applied to a broad class of canonical PDEs. For explicit and semi-implicit solvers, we consider advection-diffusion systems as well as different types of Navier-Stokes variants. We showcase models trained with up to 128 steps of a differentiable simulator and apply our model to complex three-dimensional (3D) flows, as shown in Fig. 1. Additionally, we present a detailed empirical study of different approaches for training neural networks in conjunction with iterative PDE-solvers for recurrent rollouts of several hundred time steps. On the side of implicit solvers, we consider the Poisson problem, which is an essential component of many PDE models. Here, our method outperforms existing techniques on predicting initial guesses for a conjugate gradient (CG) solver by receiving feedback from the solver at training time.

---

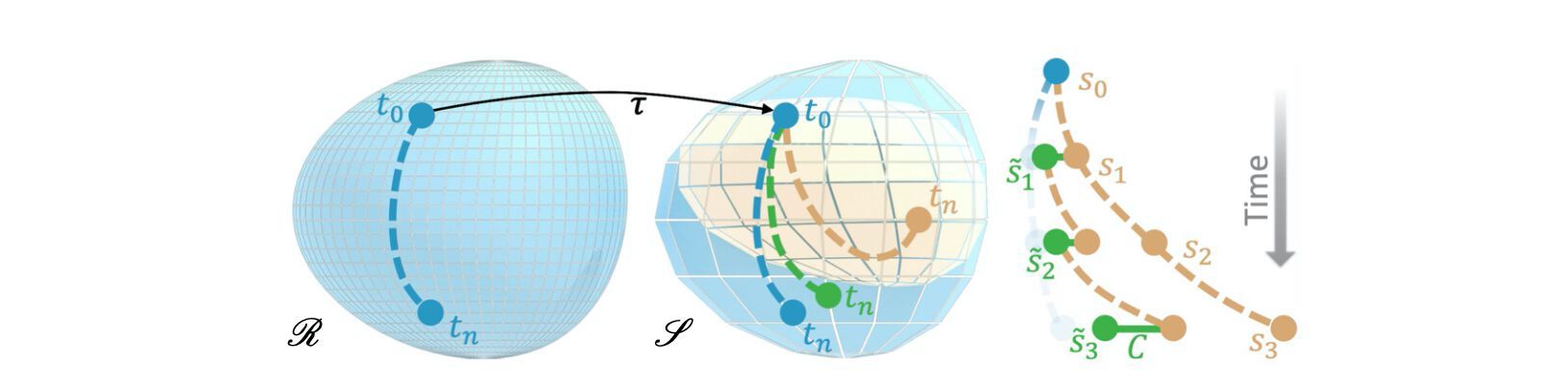
Fig. 1: Transformed solutions of the reference sequence computed on R (blue) differ from solutions computed on the source manifold S (orange). A correction function C (green) updates the state after each iteration to more closely match the projected reference trajectory on S.

---

Non-interacting (NON): The learning task purely uses the unaltered PDE trajectories with n evaluations of the PDE. These trajectories are fully contained in the source manifold S. Learning from these states means that a model will not see any states that deviate from the original solutions. As a consequence, models trained in this way can exhibit undesirably strong error accumulations over time. This corresponds to learning from the difference between the orange and blue trajectories in Fig. 1, and most commonly applied supervised approaches use this variant.

Pre-computed interaction (PRE): To let an algorithm learn from states that are closer to those targeted by the correction, i.e., the reference states, a pre-computed or analytic correction is applied. Hence, the training process can make use of phase space states that deviate from those in S, as shown in green in Fig. 1, to improve inference accuracy and stability. In this setting, the states s are corrected without employing a neural network, but they should ideally resemble the states achievable via the learned correction later on. As the modified states s are not influenced by the learning process, the training data can be pre-computed. A correction model C(s|θ) is trained that replaces the pre-computed correction at inference time.

Solver-in-the-loop (SOL): By integrating the learned function into a differentiable physics pipeline, the corrections can interact with the physical system, alter the states, and receive gradients about the future performance of these modifications. The learned function C now depends on states that are modified and evolved through P for one or more iterations. The key difference with this approach is that C is trained via s ̃, i.e., states that were affected by previous evaluations of C, and it affects s ̃ in the following iterations. As for (PRE), this learning setup results in a trajectory like the green one shown in Fig. 1, however, in contrast to before, the learned correction itself influences the evolution of the trajectory, preventing a gap for the data distribution of the inputs.

---