Thuerey Group

We would like to share our latest work: AeroTransformer — a step toward bringing the foundation model paradigm to real-world aerodynamic design.

Code & models: https://github.com/tum-pbs/AeroTransformer
Paper: https://arxiv.org/abs/2604.18062

Modern engineering workflows still rely on expensive CFD simulations — especially in 3D, where generating training data is a major bottleneck. AeroTransformer tackles this by combining large-scale pretraining + efficient fine-tuning, enabling accurate predictions with drastically reduced data requirements. Key contributions:

• A Transformer-based architecture tailored for large-scale aerodynamic learning
• Pretraining on diverse geometries (~30k samples) to capture global flow priors
• Task-specific fine-tuning with only a few hundred samples
• Establishing a pathway toward foundation models for engineering CFD

The proposed approach:

• Achieves 1.2% relative error for new geometries (drag coefficient)
• Reduces error by 84% vs training from scratch
• Demonstrates strong generalization to new wing configurations

This work reinforces a central shift: Instead of training task-specific models from scratch each time, we can pretrain once and then adapt the model with a small dataset.

Ever wondered if a Transformer model could successively refine a PDE solution? 🤔 Mario’s latest work as a post-doc at TUM shows a way forward: a single model auto-regressively infers and refines flow solutions over finer and finer sets of sample points. Preprint of this “SAR” approach and code are already online https://arxiv.org/pdf/2604.11403 and https://github.com/tum-pbs/SAR

In more detail: Understanding time-dependent fluid flows often requires knowing not just a single solution, but the full range of possible states over time. However, traditional PDE solvers are very expensive to run, and learned surrogate models that predict the next time step tend to accumulate errors when applied repeatedly over long time horizons.

Generative models offer an alternative by directly sampling flow states without relying on sequential time stepping, thereby avoiding error accumulation. However, existing approaches such as diffusion or flow-matching models remain computationally costly, as they require many evaluations across the entire spatial domain.

Scale-Autoregressive Modeling (SAR) addresses this limitation by generating flow fields in a hierarchical, coarse-to-fine manner. It first predicts a low-resolution version of the flow and then progressively refines it to higher resolutions, conditioning each step on the previous, coarser prediction. This strategy improves efficiency by focusing most of the computational effort on coarse scales—where uncertainty is highest. Importantly, it requires fewer denoising steps at finer scales.

Across unsteady-flow benchmarks of varying complexity, SAR attains substantially lower distributional error and higher per-sample accuracy than state-of-the-art diffusion models based on multi-scale GNNs, while matching or surpassing a flow-matching transformer, yet running 2-7x faster than it depending on the task. Overall, SAR provides a practical tool for fast and accurate estimation of statistical flow quantities (e.g., turbulent kinetic energy and two-point correlations) in real-world settings.

We’d like to highlight the code release of our scalable & efficient PDE Transformer (P3D) at https://akanota.github.io/p3d/ , great work Benjamin with support from Florian & Georg. Please try out the pretrained models, and let us know how it works! Highlights are, e.g., stable inference of 1024^3 rollouts on a single GPU with 90GB.

Key Contributions:

• Hybrid CNN-Transformer: P3D combines convolutions for fast local features with windowed self-attention for deep representation learning in a hierarchical U-shape structure.
• Scalable Pretraining: Pretrain on small 128³ crops, then scale to the full 1024³ domain — reducing memory and compute while maintaining accuracy.
• Global Context Network: A sequence-to-sequence model links bottleneck layers for efficient global information processing, with region tokens for direct decoder feedback.
• Probabilistic Generation: Train P3D as a diffusion model to produce probabilistic samples of turbulent channel flows, accurately capturing flow statistics across Reynolds numbers.

Links:

• Main page: https://akanota.github.io/p3d/
• Paper: https://openreview.net/forum?id=8UdCE5nhFl
• Code: https://github.com/tum-pbs/P3D
• Weights & Data: https://huggingface.co/thuerey-group/p3d

We’re happy to report that our Physics-based Flow Matching framework got an accept for ICLR’26! We target the fundamental trade-off between physical consistency and distributional fidelity in generative modeling by proposing Physics-Based Flow Matching (PBFM): a principled framework that explicitly targets Pareto-optimal solutions between physics-constraints and data-driven objectives.

• PBFM builds on flow matching and enforces PDE and algebraic constraints during training using conflict-free gradient updates via the ConFIG optimizer. We address the long-standing Jensen’s gap by unrolling the learned dynamics during training, ensuring that physical residuals are evaluated on accurate final samples, without slowing down inference.
• Across three challenging benchmarks (Darcy, Kolmogorov flows, and highly nonlinear dynamic stall), PBFM consistently advances the Pareto front, achieving lower physical residuals and better distributional accuracy than prior physics-informed diffusion and flow-based methods. At the same time, it preserves the key advantage of flow matching: fast, scalable inference, with performance comparable to unconstrained generators.
• We frame physics-constrained generative modeling as a multi-objective optimization problem to deliver a practical solution. PBFM demonstrates that high-fidelity uncertainty-aware generative models can be both physically meaningful and statistically correct; this makes them a powerful tool for real-world applications in science and engineering.

Code and paper can be found here: https://github.com/tum-pbs/PBFM/ , https://arxiv.org/abs/2506.08604

Fast rotational equivariance for physics GNNs: The source code for our paper on Rotational Equivariant GraphNets via local Eigenbases is now available: https://github.com/tum-pbs/strain-base-gnn

* We introduce a basis-transformation approach (SB-GNNs) that preserves full geometric and physical information while avoiding the heavy computational cost of conventional equivariant layers.

* Across three challenging PDE benchmarks, our method matches SOTA accuracy, consistently outperforms data augmentation, and delivers order-of-magnitude efficiency gains in practice.

* If you’re interested in ML for PDEs, CFD, or equivariant learning, the code and test cases are ready to use and build upon. Let us know how it works for you!

Please check out the full Physics-of-Fluids paper here: https://pubs.aip.org/aip/pof/article/37/8/087178/3359552/Rotational-equivariant-graph-neural-networks-via

We’re very excited to report that our P3D Transformer was accepted at ICLR https://openreview.net/forum?id=8UdCE5nhFl

• In the paper we introduce a scalable hybrid CNN–Transformer architecture that pushes neural surrogate modeling into the regime of truly high-resolution 3D simulations. By combining fast local convolutions with carefully designed attention and an optional global context model, the P3D architecture overcomes previous memory and compute barriers that have limited Transformers for PDE problems.
• P3D is trained on small 3D “crops”, but seamlessly assembles them into coherent, large-scale solutions. We show that P3D can learn multiple different types of PDE dynamics in 3D simultaneously and that it outperforms state-of-the-art neural operators and transformers in both accuracy and efficiency.
• Beyond deterministic prediction, P3D also works as a probabilistic generative model: trained via flow-matching diffusion, it produces high-fidelity samples of turbulent channel flows across varying Reynolds numbers, capturing correct velocity profiles and higher-order statistics (while being orders-of-magnitude faster than DNS).

Code and pre-trained models will be up soon!

Thanks again to the NHR@FAU HPC Center and its team for the support! It was great that we received compute time on Helma for this project. Impressive performance 🙂 👍

I’m very happy to report that our autoregressive predictions with generative diffusion models is finally accepted 😁 Congratulations Georg!

It’s been a long journey, this paper was first submitted to NeurIPS’23, and now, almost three years later and after several other stages, finally got into “Neural Networks” https://www.sciencedirect.com/science/article/pii/S0893608026001036

Despite the long wait, I think the main conclusions of our paper are still valid:

• even vanilla diffusion / flow matching models, without special modifications, perform great for time predictions
• deterministic models with proper unrolling can match them
  Importantly, both can lead to “unconditionally stable” surrogates, ie, NN operators that don’t blow up

Code & benchmark can be found here: https://github.com/tum-pbs/autoreg-pde-diffusion

There is enormous potential for reinforcement learning and other data-driven control paradigms for controlling large scale fluid flows. But RL research on such systems is often hindered by a complex and brittle software pipeline consisting of external solvers and multiple code bases, making this exciting field inaccessible for many RL researchers.

To tackle this challenge, we (primarily Jannis from TU Dortmund) have developed a standalone, fully differentiable, plug-and-play benchmark for RL in active flow control, implemented in a single PyTorch codebase via PICT, without external solver dependencies.

Our FluidGym comes with a collection of standardized environment configurations spanning diverse 3D and multi-agent control tasks. We perform an extensive experimental study with multiple seeds, randomized initial conditions and separate train/validate/test sets. We compare the default implementations of the two most popular algorithms PPO and SAC in the single and multi-agent settings, and also investigate the potential for transfer learning.

We hope that this may be of interest to a large number of reinforcement learning researchers who are keen on assessing the most recent trends in basic RL research on a new set of challenging tasks, but otherwise find it difficult to enter the field of fluid mechanics.

Repository: https://github.com/safe-autonomous-systems/fluidgym
Paper: https://arxiv.org/abs/2601.15015

Our paper on physics-constrained reconstruction / super-resolution with generative models was posted online now at https://doi.org/10.1063/5.0304492

This paper started out as a master thesis by Marc Trepat, was continued with Luis‘ thesis, and turned out to work exceptionally well:

• PDE Transformer as an accurate & efficient backbone architecture https://tum-pbs.github.io/pde-transformer/landing.html
• Differentiable physics constraints to guide the generative model https://ge.in.tum.de/publications/2020-um-solver-in-the-loop/
• and ConFIG as optimizer to resolve conflicts in the gradients https://tum-pbs.github.io/ConFIG/

Source code is available at https://github.com/tum-pbs/sparse-reconstruction , let us know how it works for you.

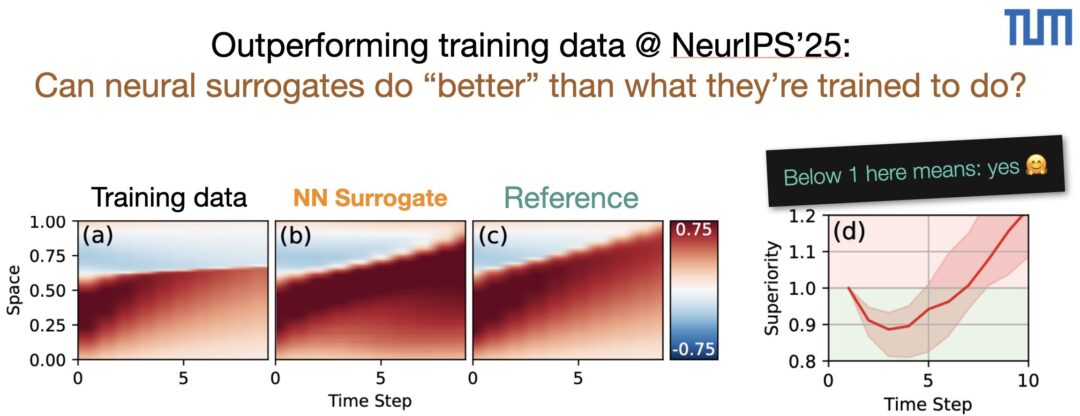
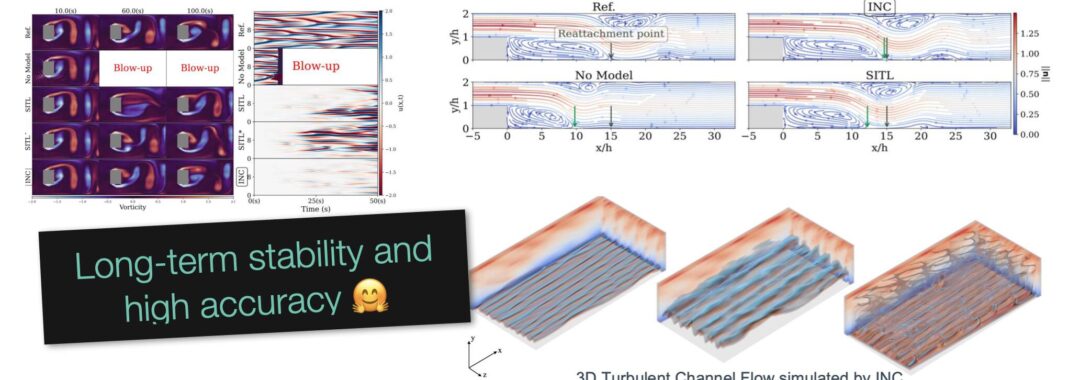
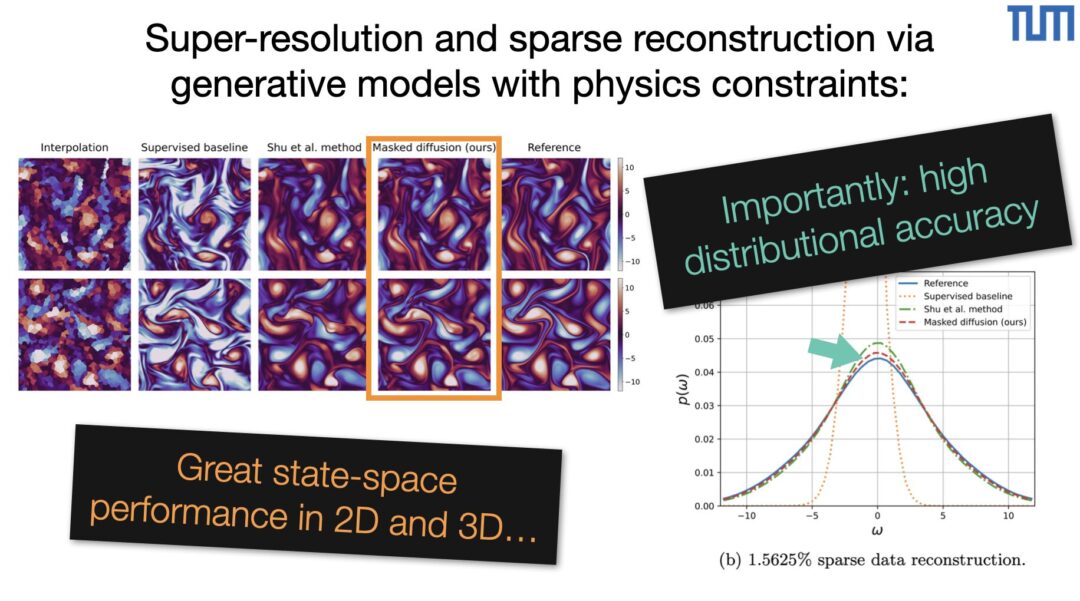
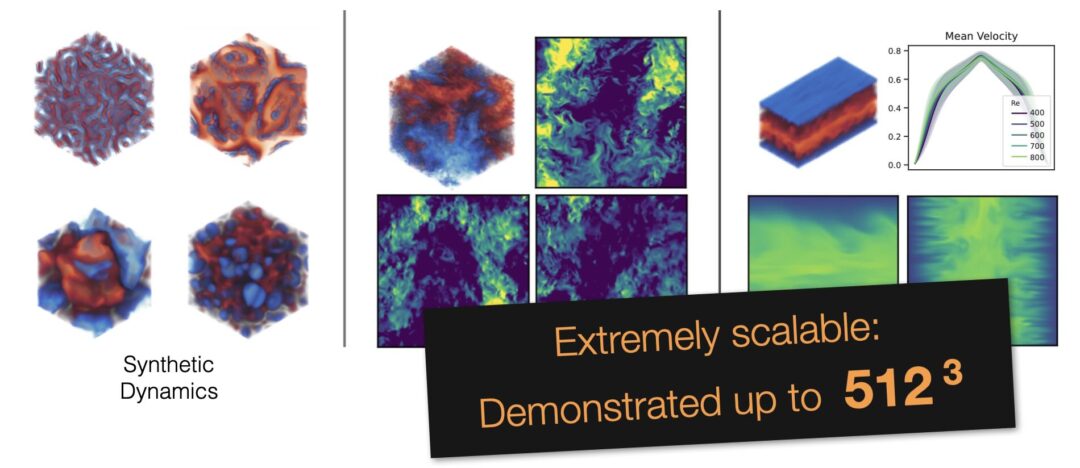
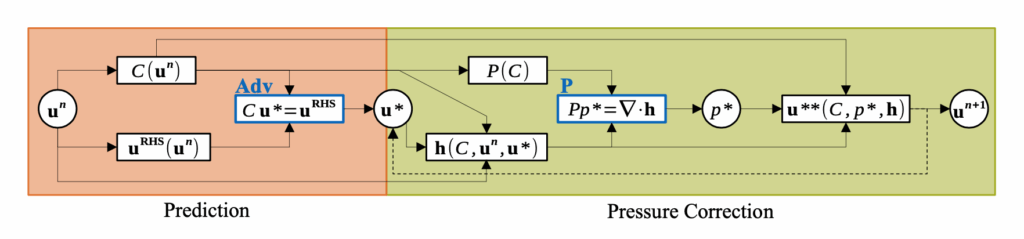
The SuperWing dataset is a large-scale, open dataset of transonic swept-wing aerodynamics, combining thousands of richly parameterized 3D wing geometries with high-fidelity RANS simulations across the operational flight envelope: https://arxiv.org/abs/2512.14397 It offers more complex geometry (“kinked” wings) and larger parametric variety than all existing 3D airfoil datasets!

Created primarily by Yunjia and collaborators from Tsinghua University, the HuggingFace dataset https://huggingface.co/datasets/yunplus/SuperWing captures strong and challenging variations in spanwise shape, twist, and dihedral angles, offering unprecedented geometric diversity. Transformer models trained on SuperWing achieve low drag-prediction errors and show strong zero-shot generalization to canonical aircraft configurations, positioning SuperWing as a key resource for data-driven aerodynamic modeling.

Full abstract: Machine-learning surrogate models have shown promise in accelerating aerodynamic design, yet progress toward generalizable predictors for three-dimensional wings has been limited by the scarcity and restricted diversity of existing datasets. Here, we present SuperWing, a comprehensive open dataset of transonic swept-wing aerodynamics comprising 4,239 parameterized wing geometries and 28,856 Reynolds-averaged Navier-Stokes flow field solutions. The wing shapes in the dataset are generated using a simplified yet expressive geometry parameterization that incorporates spanwise variations in airfoil shape, twist, and dihedral, allowing for an enhanced diversity without relying on perturbations of a baseline wing. All shapes are simulated under a broad range of Mach numbers and angles of attack covering the typical flight envelope. To demonstrate the dataset’s utility, we benchmark two state-of-the-art Transformers that accurately predict surface flow and achieve a 2.5 drag-count error on held-out samples. Models pretrained on SuperWing further exhibit strong zero-shot generalization to complex benchmark wings such as DLR-F6 and NASA CRM, underscoring the dataset’s diversity and potential for practical usage.

Can AI surrogates outperform their training data? Turns out the answer is yes – with a few caveats 😉 https://tum-pbs.github.io/emulator-superiority/ This post higlights Felix’ NeurIPS paper to be presented next week in San Diego. He discovered this “superiority”, and developed a theory to analyze when it does show up. This surprising behavior leads to interesting and fundamental questions about the role of training data, and about how neural networks and learning-based surrogates should be evaluated.

Paper abstract: Neural operators or emulators for PDEs trained on data from numerical solvers are conventionally assumed to be limited by their training data’s fidelity. We challenge this assumption by identifying “emulator superiority,” where neural networks trained purely on low-fidelity solver data can achieve higher accuracy than those solvers when evaluated against a higher-fidelity reference. Our theoretical analysis reveals how the interplay between emulator inductive biases, training objectives, and numerical error characteristics enables superior performance during multi-step rollouts. We empirically validate this finding across different PDEs using standard neural architectures, demonstrating that emulators can implicitly learn dynamics that are more regularized or exhibit more favorable error accumulation properties than their training data, potentially surpassing training data limitations and mitigating numerical artifacts. This work prompts a re-evaluation of emulator benchmarking, suggesting neural emulators might achieve greater physical fidelity than their training source within specific operational regimes.

Congratulations to Hao, Aleksandra and Bjoern for their NeurIPS paper: https://tum-pbs.github.io/inc-paper/ 👍 It analyzes how hybrid PDE solvers fundamentally and provably benefit from “indirect” (force-based) corrections rather than direct (explicit) ones. Baking the corrections into governing equations via our method, dubbed “Indirect Neural Corrections” (INC), reduces error growth without restricting architectures or solvers. Across systems from 1D chaos to 3D turbulence, INC stabilizes rollouts, prevents blowups, and delivers very substantial speed-ups—sometimes by orders of magnitude.

The full source code is already available at: https://github.com/tum-pbs/INC/

And the arXiv preprint at: https://arxiv.org/abs/2511.12764

We believe both the theory and core approach are important steps forward for combining modern AI with classic numerical solvers, opening the door to robust scientific and engineering models at scale.

Full paper abstract: When simulating partial differential equations, hybrid solvers combine coarse numerical solvers with learned correctors. They promise accelerated simulations while adhering to physical constraints. However, as shown in our theoretical framework, directly applying learned corrections to solver outputs leads to significant autoregressive errors, which originate from amplified perturbations that accumulate during long-term rollouts, especially in chaotic regimes.

To overcome this, we propose the Indirect Neural Corrector (INC), which integrates learned corrections into the governing equations rather than applying direct state updates. Our key insight is that INC reduces the error amplification on the order of (1/dt)+L, where dt is the timestep and L the Lipschitz constant. At the same time, our framework poses no architectural requirements and integrates seamlessly with arbitrary neural networks and solvers. We test in extensive benchmarks, covering numerous differentiable solvers, neural backbones, and test cases ranging from a 1D chaotic system to 3D turbulence.

INC improves the long-term trajectory performance (R^2) by up to 158%, stabilizes blowups under aggressive coarsening, and for complex 3D turbulence cases yields speed-ups of several orders of magnitude. INC thus enables stable, efficient PDE emulation with formal error reduction, paving the way for faster scientific and engineering simulations with reliable physics guarantees.

We’re happy to report that our collaborative project on 3D sparse-reconstruction and super-resolution with diffusion models, physics constraints and PDE Transformers is online now as preprint http://arxiv.org/abs/2510.19971 as well as with full source code https://github.com/tum-pbs/sparse-reconstruction.

The PDE Transformer backbone https://tum-pbs.github.io/pde-transformer/landing.html works great for large-scale 3D fields with only around 1.6% coverage, and (a variant) of our ConFIG optimizer https://tum-pbs.github.io/ConFIG/ turns out to be crucial for incorporating PDE/physics constraints!

The samples below show the excellent performance for a single snapshot, and of course the distributional accuracy needs to be taken into account when targeting probabilistic tasks: the method also works remarkably well here, as shown with one example above. Please check out the paper and code and let us know how it works for you 😀

Paper abstract: The reconstruction of unsteady flow fields from limited measurements is a challenging and crucial task for many engineering applications. Machine learning models are gaining popularity in solving this problem due to their ability to learn complex patterns from data and generalize across diverse conditions. Among these, diffusion models have emerged as particularly powerful in generative tasks, producing high-quality samples by iteratively refining noisy inputs. In contrast to other methods, these generative models are capable of reconstructing the smallest scales of the fluid spectrum. In this work, we introduce a novel sampling method for diffusion models that enables the reconstruction of high-fidelity samples by guiding the reverse process using the available sparse data. Moreover, we enhance the reconstructions with available physics knowledge using a conflict-free update method during training. To evaluate the effectiveness of our method, we conduct experiments on 2 and 3-dimensional turbulent flow data. Our method consistently outperforms other diffusion-based methods in predicting the fluid’s structure and in pixel-wise accuracy. This study underscores the remarkable potential of diffusion models in reconstructing flow field data, paving the way for their application in Computational Fluid Dynamics research.

We’re happy to introduce P3D: our PDE-Transformer architecture in 3 dimensions by Benjamin, Georg & Co. Demonstrated for unprecedented 512^3 resolutions! That means the Transformer produces over 400 million degrees of freedom in one go 😀 a regime that was previously out of reach for neural surrogates. You can check out the full paper on arXiv now: http://arxiv.org/abs/2509.10186

Of course, the model is diffusion-ready, as we show with a probabilistic, turbulent channel flow scenario. We also showcase a multi-PDE scenario with wide-ranging dynamics.

Key for the approach is a modular, pre-trained PDE-Transformer, multiple instances of which are combined or optionally via a “context model”. Paving the way for large-scale neural simulations in the future!

We’d like to thank the NHR@FAU HPC Center, for the flexible support and great hardware. The large-scale training runs of this project would not have been possible otherwise.

Full abstract: We present a scalable framework for learning deterministic and probabilistic neural surrogates for high-resolution 3D physics simulations. We introduce a hybrid CNN-Transformer backbone architecture targeted for 3D physics simulations, which significantly outperforms existing architectures in terms of speed and accuracy. Our proposed network can be pretrained on small patches of the simulation domain, which can be fused to obtain a global solution, optionally guided via a fast and scalable sequence-to-sequence model to include long-range dependencies. This setup allows for training large-scale models with reduced memory and compute requirements for high-resolution datasets. We evaluate our backbone architecture against a large set of baseline methods with the objective to simultaneously learn the dynamics of 14 different types of PDEs in 3D. We demonstrate how to scale our model to high-resolution isotropic turbulence with spatial resolutions of up to 512^3. Finally, we demonstrate the versatility of our network by training it as a diffusion model to produce probabilistic samples of highly turbulent 3D channel flows across varying Reynolds numbers, accurately capturing the underlying flow statistics.

Bjoern’s paper on equivariant GraphNets was accepted now at Physics of Fluids 👍 , you can check it out at: https://doi.org/10.1063/5.0279499 (Rotational Equivariant Graph Neural Networks via local Eigenbasis Transformations)

The core idea is a very generic and powerful one: we compute a local Eigenbasis from flow features for equivariance. Mathematically it’s identical to previous approaches, but much faster (and simpler 😅)

Full abstract: Rotational equivariance arises in physical problems as a common symmetry of partial differential equations, including the Navier–Stokes equations governing fluid phenomena. Architectural changes are necessary when guaranteeing rotational equivariance in neural networks, which incur additional computational costs, leading to increased inference times by up to an order of magnitude, as measured in our numerical studies. We introduce a new method for rotational equivariance in graph neural networks that achieves high predictive accuracy while maintaining a smaller computational footprint than comparable approaches. We establish rotational equivariance by transforming vector features and spatial neighborhood information into local, node-specific vector bases. The resulting architecture follows an encode-process-decode paradigm. Vector features are transformed before being encoded. When message-passing, i.e., in the process stage, latent features are interpreted as a set of vectors and undergo a similar transformation and are thus always processed in the receivers’ basis. The results are transformed back into the reference system after decoding, resulting in rotational equivariance. The networks receive full physical and geometric information of the neighborhood without costly computations. Three different scenarios are experimentally investigated, ranging from an advection problem to incompressible Navier–Stokes flow around an ellipse and to a highly complex transonic cylinder flow scenario. We compare with state-of-the-art approaches and demonstrate how our method achieves comparable accuracy while reducing computational costs. Our method is the only one to consistently improve upon a data-augmentation baseline, and does so with an error reduction of 25.3%. It is 1.6 times faster than the next best model that guarantees equivariance.

Our paper detailing the differentiable SPH solver by Rene is online now on arxiv: https://arxiv.org/abs/2507.21684 If you’re interested in fast and efficient neighborhoods, differentiable SPH operators and neat first optimization and learning tasks, please take a look!

Title: diffSPH: Differentiable Smoothed Particle Hydrodynamics for Adjoint Optimization and Machine Learning

Full paper abstract: We present diffSPH, a novel open-source differentiable Smoothed Particle Hydrodynamics (SPH) framework developed entirely in PyTorch with GPU acceleration. diffSPH is designed centrally around differentiation to facilitate optimization and machine learning (ML) applications in Computational Fluid Dynamics~(CFD), including training neural networks and the development of hybrid models. Its differentiable SPH core, and schemes for compressible (with shock capturing and multi-phase flows), weakly compressible (with boundary handling and free-surface flows), and incompressible physics, enable a broad range of application areas. We demonstrate the framework’s unique capabilities through several applications, including addressing particle shifting via a novel, target-oriented approach by minimizing physical and regularization loss terms, a task often intractable in traditional solvers. Further examples include optimizing initial conditions and physical parameters to match target trajectories, shape optimization, implementing a solver-in-the-loop setup to emulate higher-order integration, and demonstrating gradient propagation through hundreds of full simulation steps. Prioritizing readability, usability, and extensibility, this work offers a foundational platform for the CFD community to develop and deploy novel neural networks and adjoint optimization applications.

Our new NN architecture tailored to scientific tasks is online now, ready to be presented at ICML. It combines hierarchical processing (UDiT), scalability (SWin) and flexible conditioning mechanisms. Our ICML paper shows it outperforming existing SOTA architectures thanks to its custom combination of vision tricks. Code is up, everything ready to be presented in Vancouver by Benjamin soon 😁

Paper, code and tutorials are available at https://tum-pbs.github.io/pde-transformer/landing.html

Full abstract: We introduce PDE-Transformer, an improved transformer-based architecture for surrogate modeling of physics simulations on regular grids. We combine recent architectural improvements of diffusion transformers with adjustments specific for large-scale simulations to yield a more scalable and versatile general-purpose transformer architecture, which can be used as the backbone for building large-scale foundation models in physical sciences.
We demonstrate that our proposed architecture outperforms state-of-the-art transformer architectures for computer vision on a large dataset of 16 different types of PDEs. We propose to embed different physical channels individually as spatio-temporal tokens, which interact via channel-wise self-attention. This helps to maintain a consistent information density of tokens when learning multiple types of PDEs simultaneously.
Our pre-trained models achieve improved performance on several challenging downstream tasks compared to training from scratch and also beat other foundation model architectures for physics simulations.

We’re excited to share our latest work combining physics priors with probabilistic models: Flow Matching Meets PDEs – A Unified Framework for Physics-Constrained Generation , by Giacomo Baldan and Qiang Liu.

You can check out the full paper here! Central lessons learned are:

• Conflict-free updates are crucial for achieving very high physics-residual accuracies ✅
• Differentiable solvers can fundamentally enhance the distributional accuracy of the models ⭐️

Full paper abstract: Generative machine learning methods, such as diffusion models and flow matching, have shown great potential in modeling complex system behaviors and building efficient surrogate models. However, these methods typically learn the underlying physics implicitly from data. We propose Physics-Based Flow Matching (PBFM), a novel generative framework that explicitly embeds physical constraints, both PDE residuals and algebraic relations, into the flow matching objective. We also introduce temporal unrolling at training time that improves the accuracy of the final, noise-free sample prediction. Our method jointly minimizes the flow matching loss and the physics-based residual loss without requiring hyperparameter tuning of their relative weights. Additionally, we analyze the role of the minimum noise level, σmin, in the context of physical constraints and evaluate a stochastic sampling strategy that helps to reduce physical residuals. Through extensive benchmarks on three representative PDE problems, we show that our approach yields up to an 8× more accurate physical residuals compared to FM, while clearly outperforming existing algorithms in terms of distributional accuracy. PBFM thus provides a principled and efficient framework for surrogate modeling, uncertainty quantification, and accelerated simulation in physics and engineering applications.

While most numerical solvers focus on moving forward, sometimes you need to take a step back. Have you ever faced challenges like these?

• Solving Lagrangian inverse problems without an adjoint solver?
• Performing shape optimization, but your boundaries are non-differentiable?
• Building closure models when your SPH solver lacks gradients?

If you answered yes to any of these or similar questions, we’re excited to announce the first public release of Rene’s DiffSPH, our differentiable Smoothed Particle Hydrodynamics solver. DiffSPH can tackle all these challenges and more. It supports compressible, weakly-compressible, and incompressible fluids, all while being fully differentiable and written in PyTorch.

• Explore our repository: https://diffSPH.fluids.dev
• Check out a short live demo of a 1D Sod Shock Tube simulation in Colab

Our SIGGRAPH ’25 paper on super-large scale FLIP simulations with two-phases is online now. Bernhard’s solver is especially impressive given the fact that it’s all running on a single workstations, without GPU-support. The preview image above doesn’t do the simulations justice. Please enjoy the video in full-screen and high-quality via the link below:

• Video with additional Simulations
• Paper preprint
• MSBG Source-code

Full paper abstract: Capturing the visually compelling features of large-scale water phenomena,such as the spray clouds of crashing waves, stormy seas, or waterfalls, involves simulating not only the water but also the motion of the air interacting with it. However, current solutions in the visual effects industry still largely rely on single-phase solvers and non-physical “white-water” heuristics. To address these limitations, we present Phase-Field-FLIP (PF-FLIP), a hybrid Eulerian/Lagrangian method for the fully physics-based simulation of very large-scale, highly turbulent multiphase flows at high Reynolds numbers and high fluid density contrasts. PF-FLIP transports mass and momentum in a consistent, non-dissipative manner and, unlike most existing multiphase approaches, does not require a surface reconstruction step. Furthermore, we employ spatial adaptivity across all critical components of the simulation algorithm, including the pressure Poisson solver. We augment PF-FLIP with a dual multiresolution scheme that couples an efficient treeless adaptive grid with adaptive particles, along with a fast adaptive Poisson solver tailored for high-density-contrast multiphase flows. Our method enables the simulation of two-phase flow scenarios with a level of physical realism and detail previously unattainable in graphics, supporting billions of particles and adaptive 3D resolutions with thousands of grid cells per dimension on a single workstation.