Our paper “Numerical investigation of minimum drag profiles in laminar flow using deep learning surrogates” is online now as a preprint. It targets optimizing shapes by using trained deep neural networks models that infer manifolds of Navier-Stokes solutions. We evaluate accuracy and performance of using pretrained models to minimize the drag for shapes immersed in a moving fluid in low Reynolds number regimes.
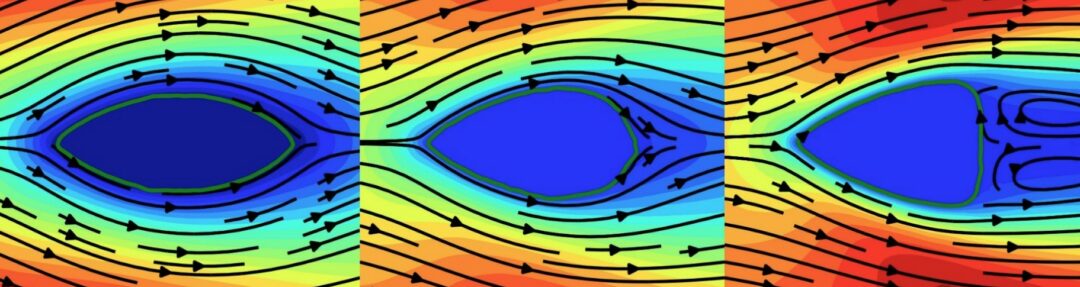
Full abstract: Efficiently predicting the flowfield and load in aerodynamic shape optimisation remains a highly challenging and relevant task. Deep learning methods have been of particular interest for such problems, due to their success for solving inverse problems in other fields. In the present study, U-net based deep neural network (DNN) models are trained with high-fidelity datasets to infer flow fields, and then employed as surrogate models to carry out the shape optimisation problem, i.e. to find a drag minimal profile with a fixed cross-section area subjected to a two-dimensional steady laminar flow. A level-set method as well as B{\’e}zier-curve method are used to parameterise the shape, while trained neural networks in conjunction with automatic differentiation are utilized to calculate the gradient flow in the optimisation framework. The optimised shapes and drag force values calculated from the flowfields predicted by DNN models agree well with reference data obtained via a Navier-Stokes solver and from the literature, which demonstrates that the DNN models are capable of predicting not only flowfield but also yield satisfactory aerodynamic forces. This is particularly promising as the DNNs were not specifically trained to infer aerodynamic forces. In conjunction with the fast runtime, the DNN-based optimisation framework shows promise for general aerodynamic design problems.