Journal of Fluid Mechanics Vol. 35
Authors Liwei Chen, Berkay A. Cakal, Xiangyu Hu, Nils Thuerey
Abstract
Efficiently predicting the flowfield and load in aerodynamic shape optimisation remains a highly challenging and relevant task. Deep learning methods have been of particular interest for such problems, due to their success for solving inverse problems in other fields. In the present study, U-net based deep neural network (DNN) models are trained with high-fidelity datasets to infer flow fields, and then employed as surrogate models to carry out the shape optimisation problem, i.e. to find a drag minimal profile with a fixed cross-section area subjected to a two-dimensional steady laminar flow. A level-set method as well as Bezier-curve method are used to parameterise the shape, while trained neural networks in conjunction with automatic differentiation are utilized to calculate the gradient flow in the optimisation framework. The optimised shapes and drag force values calculated from the flowfields predicted by DNN models agree well with reference data obtained via a Navier-Stokes solver and from the literature, which demonstrates that the DNN models are capable of predicting not only flowfield but also yield satisfactory aerodynamic forces. This is particularly promising as the DNNs were not specifically trained to infer aerodynamic forces. In conjunction with the fast runtime, the DNN-based optimisation framework shows promise for general aerodynamic design problems.
Links![]() Preprint
Preprint![]() DOI
DOI![]() Source code
Source code
Motivation
Owing to the importance in a wide range of fundamental studies and industrial applications, a significant effort has been made to study the shape optimisation for minimising aerodynamic drag over a bluff body. The deployment of computational fluid dynamics tools has played an important role in these optimisation problems. While a direct optimisation via high-fidelity computational fluid dynamics (CFD) models gives reliable results, the high computational cost of each simulation, e.g., Reynolds-averaged Navier-Stokes formulations, and the large amount of evaluations needed, lead to assessments that such optimisations are still not feasible for the practical engineering. When considering gradient-based optimisation, the adjoint method provides an effective way to calculate the gradients of an objective function w.r.t. design variables and alleviates the computational workload greatly, but the number of required adjoint CFD simulations is typically still prohibitively expensive when multiple optimisation objectives are considered. In gradient-free methods (e.g. genetic algorithm), the computational cost rises dramatically as the number of design variables is increased, especially when the convergence requirement is tightened. Therefore, advances in terms of surrogate-based optimisation are of central importance for both gradient-based and gradient-free optimisation methods.
In the present paper, we adopt an approach for the U-net based flowfield inference (Thuerey et al. 2018) and use the trained deep neural network as flow solver in the shape optimisation. In comparison to conventional surrogate models and other optimisation work involving deep learning, we make use of a generic model that infers flow solutions: in our case it produces fluid pressure and velocity as field quantities. I.e., given encoded boundary conditions and shape, the DNN surrogate produces a flowfield solution, from which the aerodynamic forces are calculated. Thus, both the flowfield and aerodynamic forces can be obtained during the optimisation. As we can fully control and generate arbitrary amounts of high-quality flow samples, we can train our models in a fully supervised manner. We use the trained DNN models in the shape optimisation to find the drag minimal profile in the two-dimensional steady laminar flow regime for a fixed cross-section area, and evaluate results w.r.t. shapes obtained using a full Navier-Stokes flow solver in the same optimisation framework. Both level-set and Bézier-curve based methods are employed for shape parameterisation. The implementation utilizes the automatic differentiation package of the PyTorch package, so the gradient flow driving the evolution of shapes can be directly calculated. Here DNN-based surrogate models show particular promise as they allow for a seamless integration into the optimisation algorithms that are commonly used for training DNNs.
The purpose of the present work is to demonstrate the capability of deep learning techniques for robust and efficient shape optimisation, and for achieving an improved understanding of the inference of the fundamental phenomena involved in these kinds of flows.
Highlights
Deep neural networks are used as surrogate models to carry out shape optimisation for drag minimisation of the flow past a profile with a given area subjected to the two-dimensional incompressible fluid at low Reynolds numbers. Both level-set and Bézier curve representations are adopted to parameterise the shape, the integral values on the re-sampled Cartesian mesh are used as the optimisation objective. The gradient flow that drives the evolution of shape profile is calculated by automatic differentiation in a deep learning framework, which seamlessly integrates with trained neural network models.
| Name | # of flowfields | Reynolds number | NN models |
| Dataset-1 | 2500 | 1 | small, medium & large |
| Dataset-40 | 2500 | 40 | small, medium & large |
| Dataset-Range | 3028 | 0.5 – 42.5 | large |
Tab. 1: Three datasets for training the neural network models.
We obtained seven neural network models shown in table 1, i.e. models of three network sizes for “Dataset-1” and “Dataset-40” and a ranged model trained with “Dataset-Range”. These neural networks are used as surrogate models in the optimisation and the results are also compared to that using OpenFOAM.
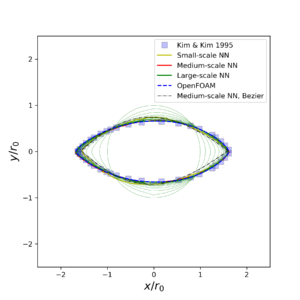
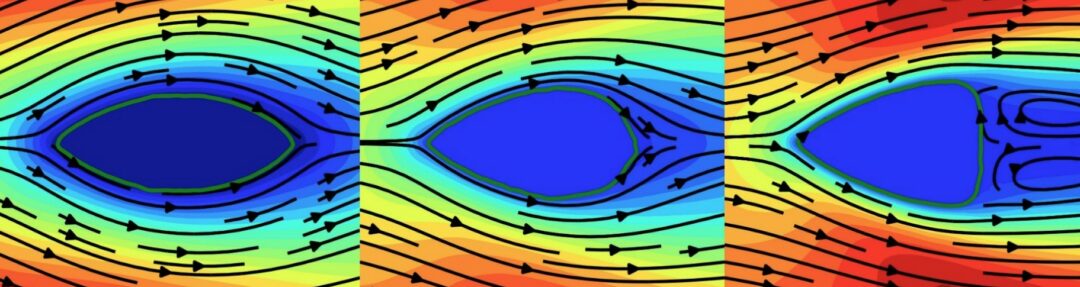
Fig. 1: The converged shapes at Re=1 with intermediate states predicted
by large-scale neural network model at every 10th iteration.
Figure 1 depicts the converged shapes of all four solvers at Re = 1. For comparison, the Bézier curve based result is also shown. In this case, the NN models are trained with Dataset-1. The ground truth result using OpenFOAM ends up with a rugby shape which achieves a good agreement with the data by Kim & Kim (2005). The medium and large-scale neural network models collapse and compare favourably with the ground truth result.
The generalising capabilities of neural networks are a challenging topic. To evaluate their flexibility in our context, we target shape optimisations in the continuous range of Reynolds numbers from Re = 1 to 40, over the course of which the flow patterns change significantly. Hence, in order to succeed, a neural network not only has to encode change of the solutions w.r.t. immersed shape but also the changing physics of the different Reynolds numbers. In this section, we conduct four tests at Re = 1, 5, 10, and 40 with the ranged model (trained with Dataset-Range) in order to quantitatively assess the its ability to make accurate flowfield predictions over the chosen change of Reynolds numbers. The corresponding OpenFOAM runs are used as ground truth for comparisons.
At Re = 1 and 5, the profiles converge with sharp trailing edges as depicted in figures 2(a) and 2(b). In figure 2(c) at Re = 10 and figure 2(d) at Re = 40, blunt trailing edges become the final shapes and the profile at Re = 10 is more slender than that for Re = 40.
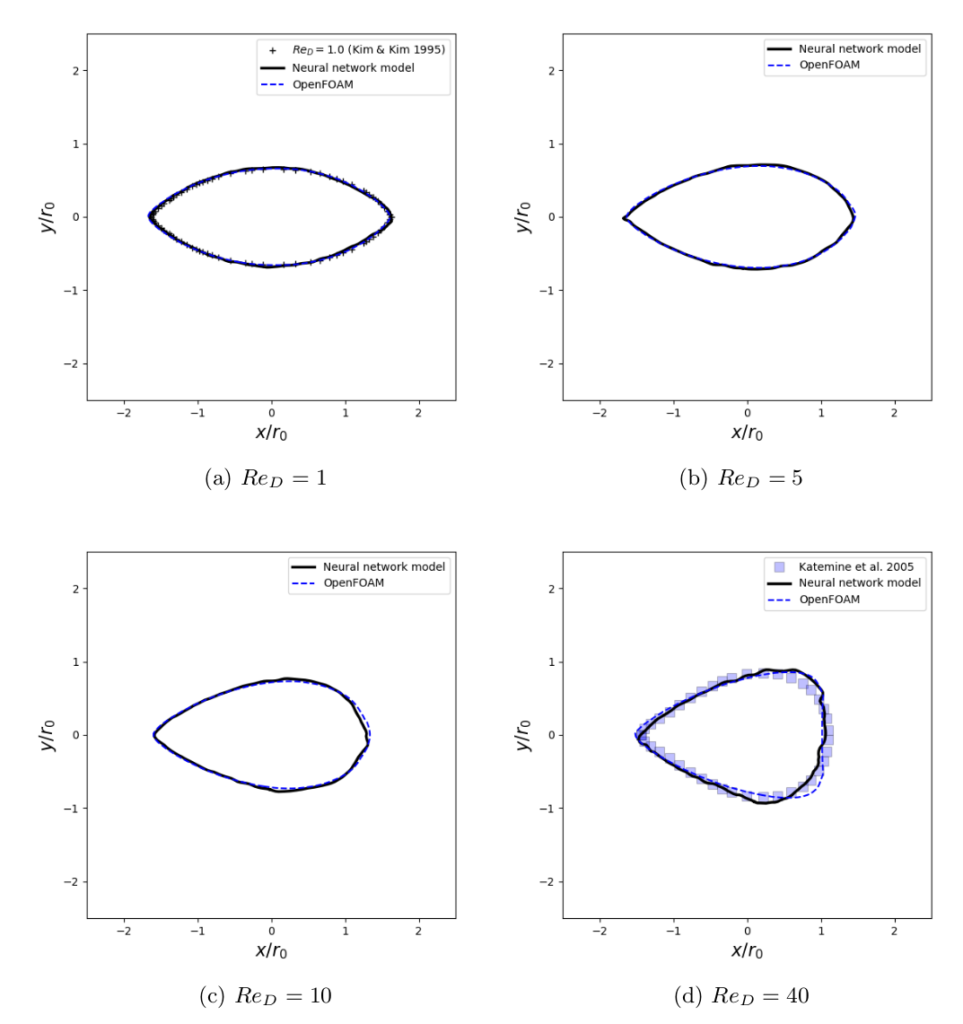
Fig. 2: Shapes after optimisation at Re = 1, 5, 10, and 40. The black solid lines denote the results using neural network models (i.e. the ranged model trained with Dataset-Range), the blue dashed lines denote the results from OpenFOAM and the symbols denote the corresponding reference data.