ACM Transactions on Graphics (SIGGRAPH). 2018; 37(4): 1-15.;  arXiv pre-print 1801.09710.

Authors
You Xie*, Technical University of Munich
Erik Franz*, Technical University of Munich
MengYu Chu*, Technical University of Munich
Nils Thuerey, Technical University of Munich
(* Similar contributions)

Abstract
We propose a temporally coherent generative model addressing the super-resolution problem for fluid flows. Our work represents the first approach to synthesize four-dimensional physics fields with neural networks. Based on a conditional generative adversarial network that is designed for the inference of three-dimensional volumetric data, our model generates consistent and detailed results by using a novel temporal discriminator, in addition to the commonly used spatial one. Our experiments show that the generator is able to infer more realistic high-resolution details by using additional physical quantities, such as low-resolution velocities or vorticities. Besides improvements in the training process and in the generated outputs, these inputs offer means for artistic control as well. We additionally employ a physics-aware data augmentation step, which is crucial to avoid overfitting and to reduce memory requirements. In this way, our network learns to generate advected quantities with highly detailed, realistic, and temporally coherent features. Our method works instantaneously, using only a single time-step of low-resolution fluid data. We demonstrate the abilities of our method using a variety of complex inputs and applications in two and three dimensions.

Links
Preprint
 Main Video, Supplemental Video
Presentation at SIGGRAPH 2018
 Code, Trained 2d model, Trained 3d model

Bibtex
@article{xie2018tempoGAN, 
title="{tempoGAN: A Temporally Coherent, Volumetric GAN for Super-resolution Fluid Flow}", 
author={Xie, You and Franz,Erik and Chu, Mengyu and Thuerey, Nils}, 
journal={ACM Transactions on Graphics (TOG)}, 
volume={37}, number={4}, pages={95}, year={2018}, publisher={ACM} }

Further Information
Generative models were highly successful in the last years to represent and synthesize complex natural images [Goodfellow et al.2014]. However, in their original form, these generative models do not take into account the temporal evolution of the data, which is crucial for realistic physical systems. In our work, we extend these methods to generate high-resolution volumetric data sets of passively advected flow quantities, and ensuring temporal coherence is one of the core aspects that we focus on. We demonstrate that it is especially important to make the training process aware of the underlying transport phenomena, such that the network can learn to generate stable and highly detailed solutions.

The main contributions of our work are:
• a novel temporal discriminator, to generate consistent and highly detailed results over time,
• artistic control of the outputs, in the form of additional loss terms and an intentional entangling of the physical quantities used as inputs,
• a physics aware data augmentation method,
• and a thorough evaluation of adversarial training processes for physics functions.

To the best of our knowledge, our approach is the first generative adversarial network for four-dimensional functions. From approximate solutions, our network successfully learns to infer solutions for flow transport processes. A preview of the architecture we propose can be found in the figure below.

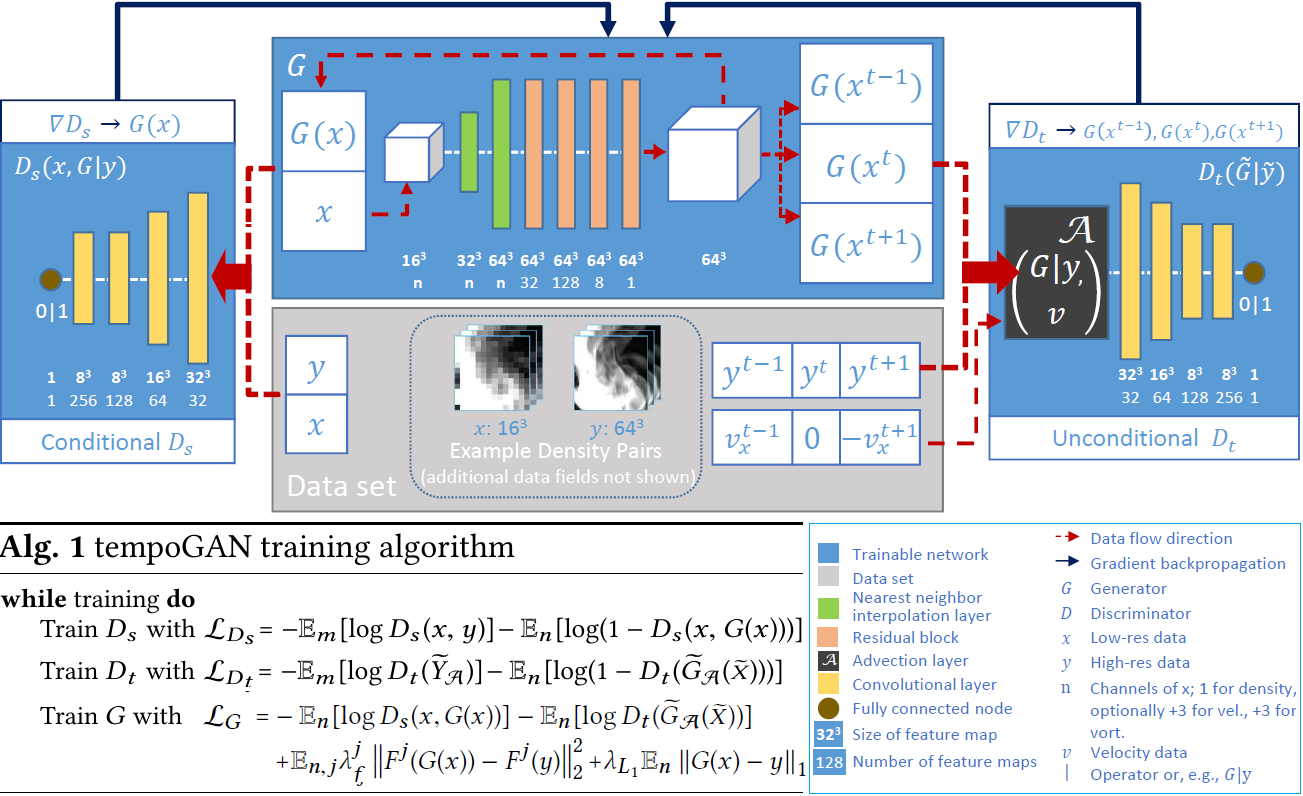
As shown in the figure, during training, we first train spatial Discriminator Ds with normal GAN loss for Discriminators. Then train our novel temporal Discriminator Dt with normal Discriminator loss but with sequence data input. We finally train our Generator with the adversarial loss from both Ds and Dt, a novel layer loss term, and a regularization l1 loss. With these losses, our generator learns to generate fluid data with highly detailed, realistic, and temporally coherent features using only a single time-step of low-resolution input.

Overall, we believe that our contributions yield a robust and very general method for generative models of physics problems, and for super-resolution flows in particular. It will be highly interesting as future work to apply our tempoGAN to other physical problem settings, or even to non-physical data such as video streams. More details are written in the paper.

This work was supported by the ERC Starting Grant 637014.