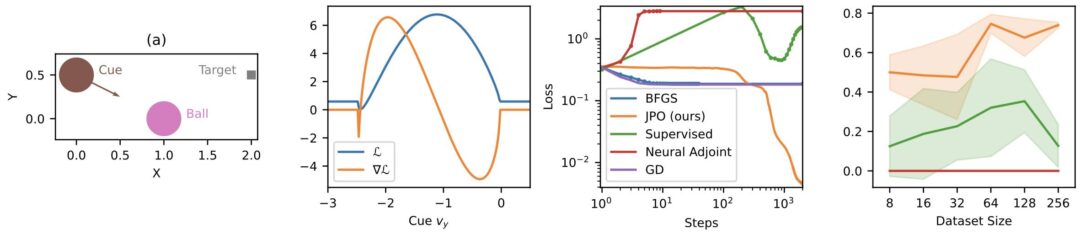
We just posted our paper on the “unreasonable” effectivness of NNs for optimization tasks: they outperform BFGS as a drop-in replacement when solving multiple problems. We can recommend giving it a try if you have an inverse problem where you’re currently using BFGS. We’d be very curious to hear how much improvements in terms of accuracy you get out of it!
Full paper: The Unreasonable Effectiveness of Solving Inverse Problems with Neural Networks , http://arxiv.org/abs/2408.08119
Paper abstract: Finding model parameters from data is an essential task in science and engineering, from weather and climate forecasts to plasma control. Previous works have employed neural networks to greatly accelerate finding solutions to inverse problems. Of particular interest are end-to-end models which utilize differentiable simulations in order to backpropagate feedback from the simulated process to the network weights and enable roll-out of multiple time steps. So far, it has been assumed that, while model inference is faster than classical optimization, this comes at the cost of a decrease in solution accuracy. We show that this is generally not true. In fact, neural networks trained to learn solutions to inverse problems can find better solutions than classical optimizers even on their training set. To demonstrate this, we perform both a theoretical analysis as well an extensive empirical evaluation on challenging problems involving local minima, chaos, and zero-gradient regions. Our findings suggest an alternative use for neural networks: rather than generalizing to new data for fast inference, they can also be used to find better solutions on known data.