We finally also have the source code for our RB-control paper online: https://github.com/tum-pbs/two-way-coupled-control , the paper being available here: https://ge.in.tum.de/download/two-way-control.pdf.
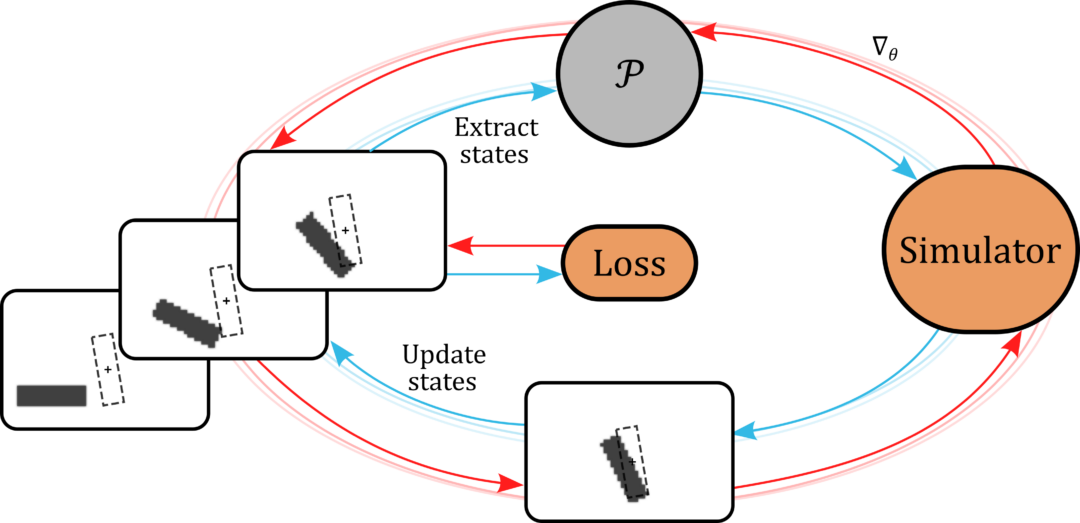
A differentiable flow solver is used to train a controller that steers a rigid body to reach a goal position and orientation. Interestingly, the differentiable solver learns much faster and more reliably than the reinforcement learning variants we tried, and it clearly outperforms simpler baselines:
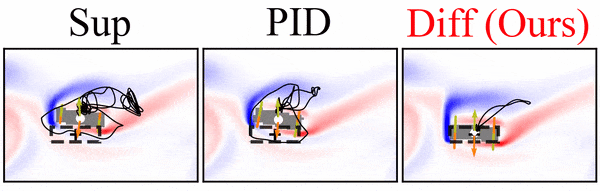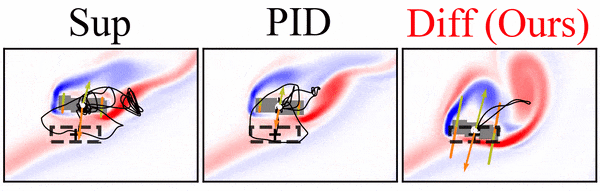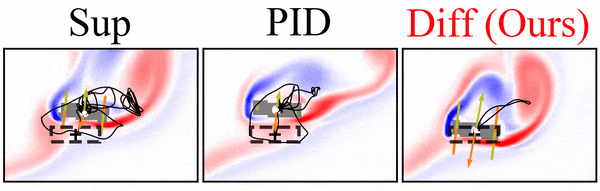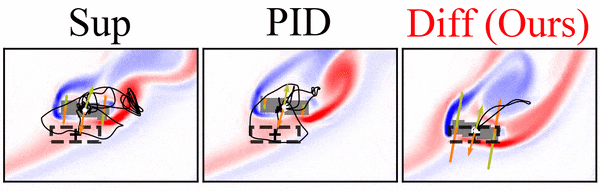
Paper abstract: We investigate the use of deep neural networks to control complex nonlinear dynamical systems, specifically the movement of a rigid body immersed in a fluid. We solve the Navier Stokes equations with two way coupling, which gives rise to nonlinear perturbations that make the control task very challenging. Neural networks are trained in an unsupervised way to act as controllers with desired characteristics through a process of learning from a differentiable simulator. Here we introduce a set of physically interpretable loss terms to let the networks learn robust and stable interactions. We demonstrate that controllers trained in a canonical setting with quiescent initial conditions reliably generalize to varied and challenging environments such as previously unseen inflow conditions and forcing, although they do not have any fluid information as input. Further, we show that controllers trained with our approach outperform a variety of classical and learned alternatives in terms of evaluation metrics and generalization capabilities.