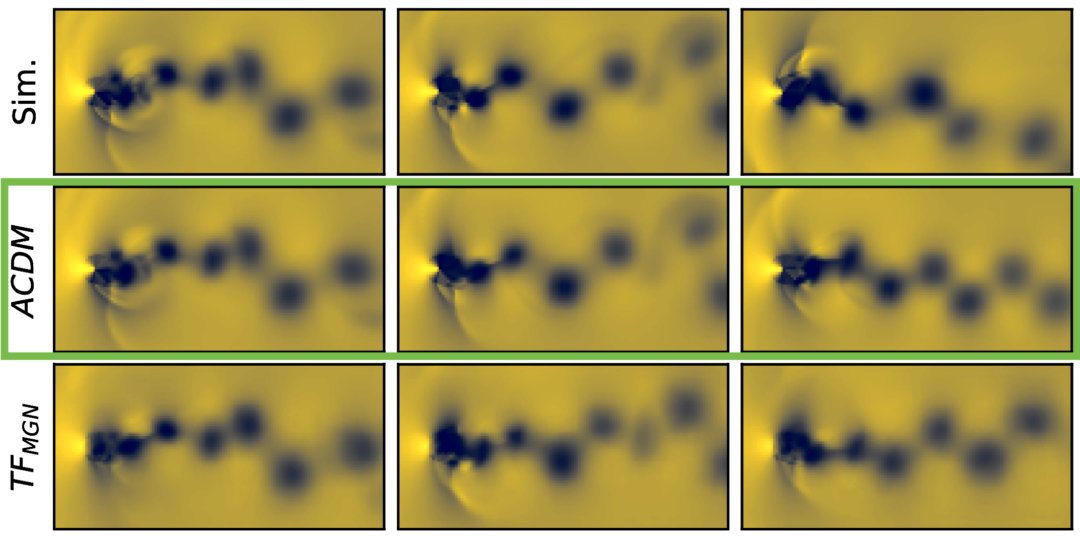
Our paper on autoregressive diffusion models for improved temporal predictions of complex PDE-based simulations is online now at https://arxiv.org/abs/2309.01745 (ACDM). Above you can see a preview output from a transonic turbulent flow case. Especially the shock waves around the obstacle are very tough here.
To summarize the results of ACDM: it’s highly accurate and turns a regular Neural PDE solver into a probabilistic method, i.e. it can compute different versions of the solution via posterior sampling. This is an example:

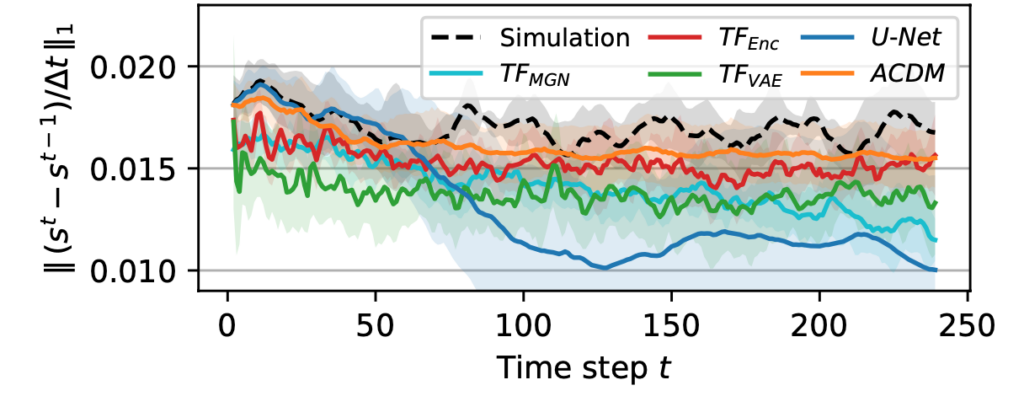
A key insight is also that the diffusion training (ACDM) yields an excellent temporal stability, despite being trained without any unrolling. Here’s a preview ACDM in orange versus a few baselines (GT in black):
Full abstract: Simulating turbulent flows is crucial for a wide range of applications, and machine learning-based solvers are gaining increasing relevance. However, achieving stability when generalizing to longer rollout horizons remains a persistent challenge for learned PDE solvers. We address this challenge by introducing a fully data-driven fluid solver that utilizes an autoregressive rollout based on conditional diffusion models. We show that this approach offers clear advantages in terms of rollout stability compared to other learned baselines. Remarkably, these improvements in stability are achieved without compromising the quality of generated samples, and our model successfully generalizes to flow parameters beyond the training regime. Additionally, the probabilistic nature of the diffusion approach allows for inferring predictions that align with the statistics of the underlying physics. We quantitatively and qualitatively evaluate the performance of our method on a range of challenging scenarios, including incompressible Navier-Stokes and transonic flows, as well as isotropic turbulence.