ACM Transactions on Graphics (SIGGRAPH) 2025
Authors
Bernhard Braun, Technical University of Munich
Jan Bender, RWTH Aachen University
Nils Thuerey, Technical University of Munich
Abstract
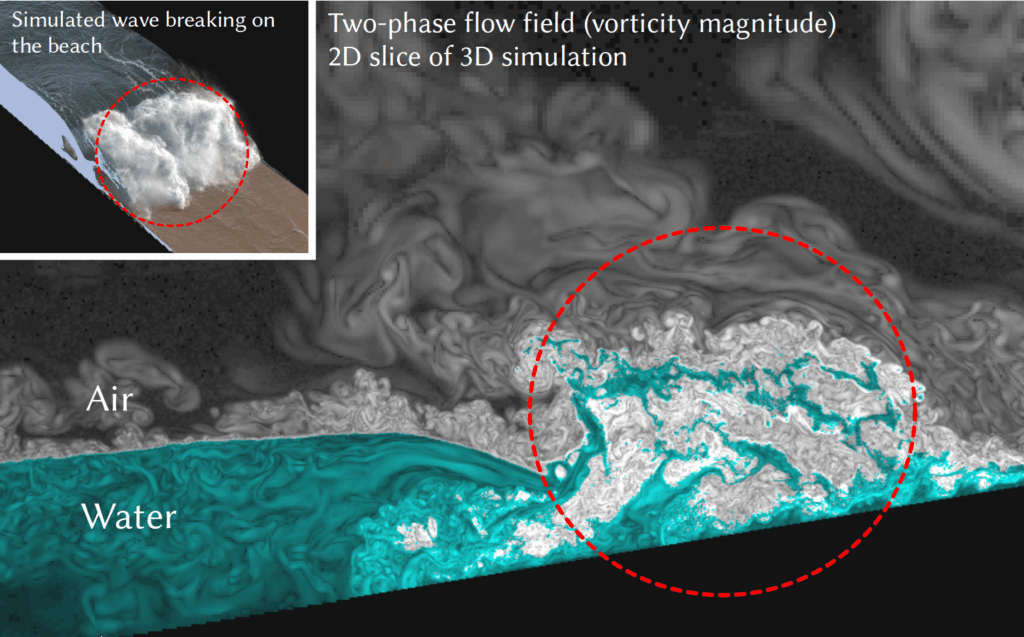
Capturing the visually compelling features of large-scale water phenomena,such as the spray clouds of crashing waves, stormy seas, or waterfalls, involves simulating not only the water but also the motion of the air interacting with it. However, current solutions in the visual effects industry still largely rely on single-phase solvers and non-physical “white-water” heuristics. To address these limitations, we present Phase-Field-FLIP (PF-FLIP), a hybrid Eulerian/Lagrangian method for the fully physics-based simulation of very large-scale, highly turbulent multiphase flows at high Reynolds numbers and high fluid density contrasts. PF-FLIP transports mass and momentum in a consistent, non-dissipative manner and, unlike most existing multiphase approaches, does not require a surface reconstruction step. Furthermore, we employ spatial adaptivity across all critical components of the simulation algorithm, including the pressure Poisson solver. We augment PF-FLIP with a dual multiresolution scheme that couples an efficient treeless adaptive grid with adaptive particles, along with a fast adaptive Poisson solver tailored for high-density-contrast multiphase flows. Our method enables the simulation of two-phase flow scenarios with a level of physical realism and detail previously unattainable in graphics, supporting billions of particles and adaptive 3D resolutions with thousands of grid cells per dimension on a single workstation.
Links
Preprint
Code for the MSBG framework
Video
Necessity of Two-Phase Simulation.
Water simulations in Graphics often neglect the air phase, assuming constant zero air pressure. In these free surface methods, the governing Navier-Stokes equations are thus solved only for the water phase. This simplification, however, becomes insufficient for large-scale phenomena where the violent motion of large masses of water induces strong movements of the surrounding air and aerodynamic forces, which scale with the square of the relative air-water velocity, become dominant. The resulting high Weber numbers inhibit surface tension from stabilizing the liquid, leading to fragmentation into spray droplets. These droplets do not simply follow ballistic trajectories; instead, they form intricate, dynamic patterns driven by the complex interplay of gravity, inertial forces and—crucially—the turbulent air velocity field. Accurately capturing these phenomena requires both modeling the coupled liquid-air velocity and a numerical method powerful enough to resolve scales ranging from tiny spray droplets to large gravity-driven waves.
