International Conference on Learning Representations (ICLR 2023)
Authors
Erik Franz, TUM
Barbara Solenthaler, ETHZ
Nils Thuerey, TUM
Abstract
We address the challenging problem of jointly inferring the 3D flow and volumetric densities moving in a fluid from a monocular input video with a deep neural network. Despite the complexity of this task, we show that it is possible to train the corresponding networks without requiring any 3D ground truth for training. In the absence of ground truth data we can train our model with observations from real-world capture setups instead of relying on synthetic reconstructions. We make this unsupervised training approach possible by first generating an initial prototype volume which is then moved and transported over time without the need for volumetric supervision. Our approach relies purely on image-based losses, an adversarial discriminator network, and regularization. Our method can estimate long-term sequences in a stable manner, while achieving closely matching targets for inputs such as rising smoke plumes.

Fig. 1: Qualitative comparison between different approaches using ScalarFlow data for after 100 time-steps. Our method closely matches the given input and has a clearly defined shape that matches the general shape of the reference. It is only surpassed by our previous, costly single-scene reconstruction method GlobTrans. RapidGen was adapted to be trained without 3D GT.
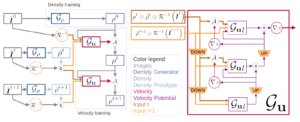
Fig. 2: Left: An overview over the complete NGT framework. We generate an initial density volume that is advected by the velocity to form a sequence. Density estimates are used in addition to the single input image to guide and stabilize the velocity generation. Velocity training is done end-to-end over the whole sequence. Right: Our multi-scale velocity estimator, shown for 3 resolution scales. The inputs contain information about the current (t) and next (t + 1) time step. Each scale generates a residual velocity potential which is used to advect the inputs of step t before generating the next residual. The final velocity is divergence free due to using the curl.

