Under Review
Authors
Georg Kohl, Technical University of Munich
Li-Wei Chen, Technical University of Munich
Nils Thuerey, Technical University of Munich
Abstract
Simulating turbulent flows is crucial for a wide range of applications, and machine learning-based solvers are gaining increasing relevance. However, achieving temporal stability when generalizing to longer rollout horizons remains a persistent challenge for learned PDE solvers. In this work, we analyze if fully data-driven fluid solvers that utilize an autoregressive rollout based on conditional diffusion models are a viable option to address this challenge. We investigate accuracy, posterior sampling, spectral behavior, and temporal stability, while requiring that methods generalize to flow parameters beyond the training regime. To quantitatively and qualitatively benchmark the performance of a range of flow prediction approaches, various challenging scenarios including incompressible and transonic flows, as well as isotropic turbulence are employed. We find that even simple diffusion-based approaches can outperform various established flow prediction methods in terms of accuracy and temporal stability, while being on par with state-of-the-art stabilization techniques like unrolling at training time. While traditional architectures are superior in terms of inference speed, the probabilistic nature of diffusion approaches allows for inferring multiple predictions that align with the statistics of the underlying physics.
Keywords
turbulent flow, PDEs, numerical simulation, diffusion models, autoregressive models
Links![]() Preprint
Preprint![]() Source Code
Source Code![]() Data and Model Download
Data and Model Download
In the following, videos for various evaluations from our work can be found. First, prediction trajectories from the different neural operator architectures are shown for each of our data sets. Second, we show posterior sampling results from the investigated probabilistic approaches. Finally, we show an evaluation regarding the temporal coherence of the ACDM approach.
Incompressible Flow Predictions
The following Videos 1 and 2 contain vorticity predictions for the incompressible flow Incvar with a changing Reynolds number over the course of the simulation time. All methods besides the FNO variants do well here.
Video 1: Zoomed predictions (vorticity) across the investigated architectures on Incvar.
Video 2: Full predictions (vorticity) for some key architectures on Incvar.
Transonic Flow Predictions
Videos 3 and 4 contain pressure predictions for the transonic flow Tralong. Note how the simulation trajectory does not follow a simple periodic oscillation, but rather exhibits highly complex and chaotic behavior caused by the interaction of the shock waves with the flow. The main methods performing well in this evaluation are the latent transformers, the U-Nets with explicit stabilization, and the ACDM variants.
Video 3: Zoomed predictions (pressure) for the investigated architectures on Tralong.
Video 4: Full predictions (pressure) for some key architectures on Tralong.
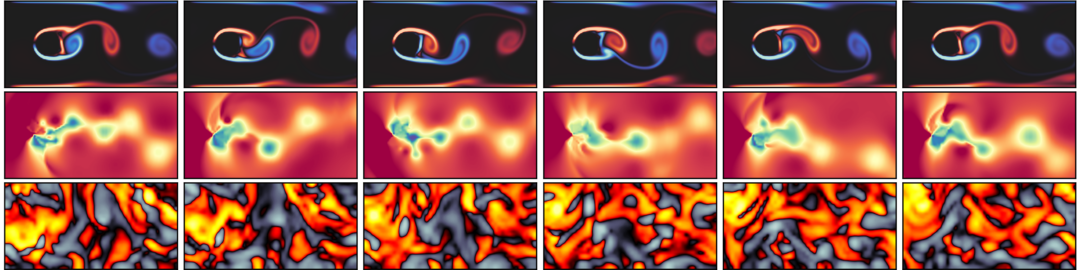
Isotropic Turbulence Predictions
Videos 5 and 6 show vorticity predictions for the isotropic turbulence case with z=260. This case is highly underdetermined and all predictions deteriorate to different degrees over the simulation rollout as a result. U-Netut, U-Nettn and ACDM perform best in this prediction task.
Video 5: Zoomed predictions (vorticity) across the investigated architectures on Iso.
Video 6: Full predictions (vorticity) for some key architectures on Iso.
Posterior Sampling
The following Videos 7, 8, and 9 analyze the posterior sampling of the probabilistic models ACDM, TFVAE, and Refiner corresponding to Section VI-B in the paper. Note how ACDM produces diverse and realistic samples, while TFVAE fails to create meaningful differences across samples. Refiner can only create minor differences between samples. In addition, the method has issues with unphyiscal and diverging predictions towards the later stages of the rollout.
Video 7: ACDM posterior samples on Tralong (pressure).
Video 8: TFVAE posterior samples on Tralong (pressure).
Video 9: Refiner posterior samples on Tralong (pressure).
Temporal Coherence of ACDM
Videos 10, 11, and 12 show the temporal coherence of ACDM predictions on Iso corresponding to the evaluation in Appendix V. Vorticity values of the predictions flucuate close to 0, leading to visual flickering in Video 10. However, as shown in Videos 11 and 12 the raw predicted velocities do not have any temporal coherence issues. The flickering is only caused by low amplitude oscillations which are amplified by the vorticity computation.
Video 10: ACDM vorticity samples on Iso exhibit minor temporal coherence issues as visual flickering.
Video 11: ACDM X-velocity samples on Iso are smooth and do not have issues with temporal coherence.
Video 12: ACDM Y-velocity samples on Iso are also smooth and do not have issues with temporal coherence.