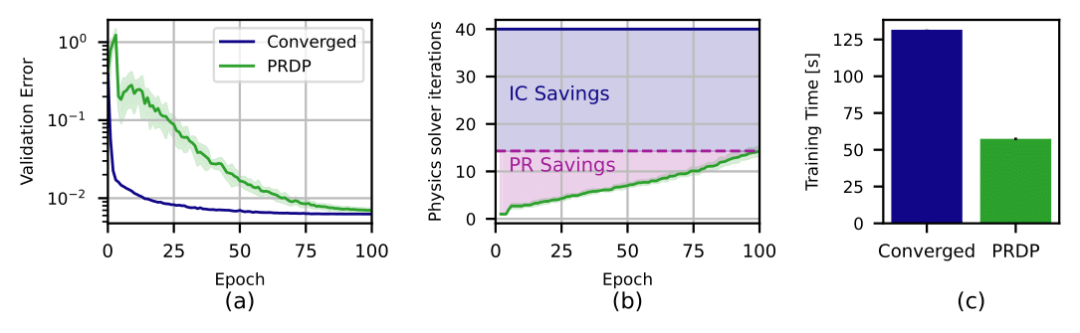
Congratulations to Kanishk and Felix 👍 for their #ICLR’25 paper “Progressively Refined Differentiable Physics” https://kanishkbh.github.io/prdp-paper/ , the key insight is that training can be accelerated substantially by using fast approximates of the gradient (especially in early phases of training).
Full paper abstract: The physics solvers employed for neural network training are primarily iterative, and hence, differentiating through them introduces a severe computational burden as iterations grow large. Inspired by works in bilevel optimization, we show that full accuracy of the network is achievable through physics significantly coarser than fully converged solvers. We propose progressively refined differentiable physics (PRDP), an approach that identifies the level of physics refinement sufficient for full training accuracy. By beginning with coarse physics, adaptively refining it during training, and stopping refinement at the level adequate for training, it enables significant compute savings without sacrificing network accuracy. Our focus is on differentiating iterative linear solvers for sparsely discretized differential operators, which are fundamental to scientific computing. PRDP is applicable to both unrolled and implicit differentiation. We validate its performance on a variety of learning scenarios involving differentiable physics solvers such as inverse problems, autoregressive neural emulators, and correction-based neural-hybrid solvers. In the challenging example of emulating the Navier-Stokes equations, we reduce training time by 62%.