TL;DR: There’s a surprising aspect of our recent paper https://arxiv.org/abs/2402.12971 that’s easy to overlook: we noticed that NN test error scales sub-optimally with -1/3 over parameter count. This is for correction, while prediction tasks are slightly worse with -1/4. Our results indicate that this is stable across physical systems and network architectures!
An obvious conclusion is that larger networks achieve better results. However, in the context of scientific computing, simply increasing the network size further and further is not an attractive option. As neural approaches compete with established numerical methods, applying pure neural or hybrid architectures always entails accuracy, efficiency, and scaling considerations. The scaling of networks towards real-world engineering problems on physical systems has been an open question, and overly large networks will be more resource hungry than established solvers in the worst case.
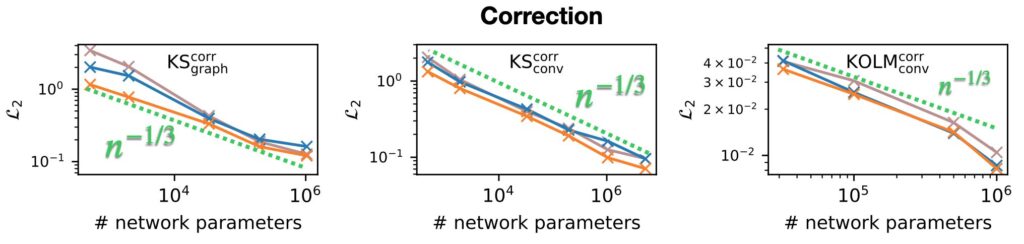
To shed light here, we computed a convergence rate between the test loss and the number of network parameters. We used an average test loss for each individual combination of network size and training setup. The average is computed over the full set of random seeds used in our study, i.e., 8 to 20 individual training runs per size and variant depending on the physical system (more than 800 models for the 3 graphs above). For the correction setups (NN+coarse solver), we estimate the convergence rate of the correction networks with respect to the parameter count n to be n^-1/3, as shown above. This means a network with twice the size only gives an error reduction of ca. 20% … that’s not a lot.
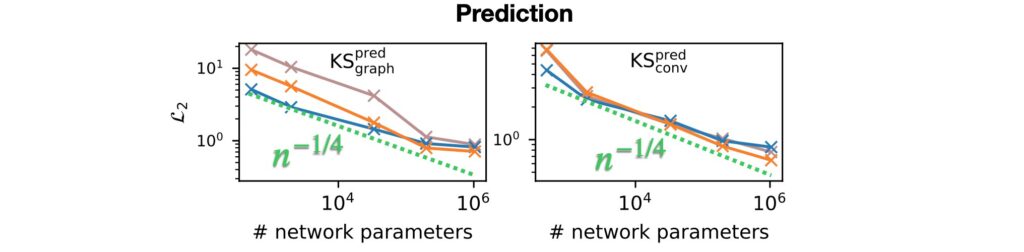
Interestingly, the measured convergence rates are agnostic to the physical system and the studied network architectures. For prediction setups (pure NN, no solver), the convergence rate of the networks with respect to the parameter count n is even slightly worse with n^-1/3 , as shown below.
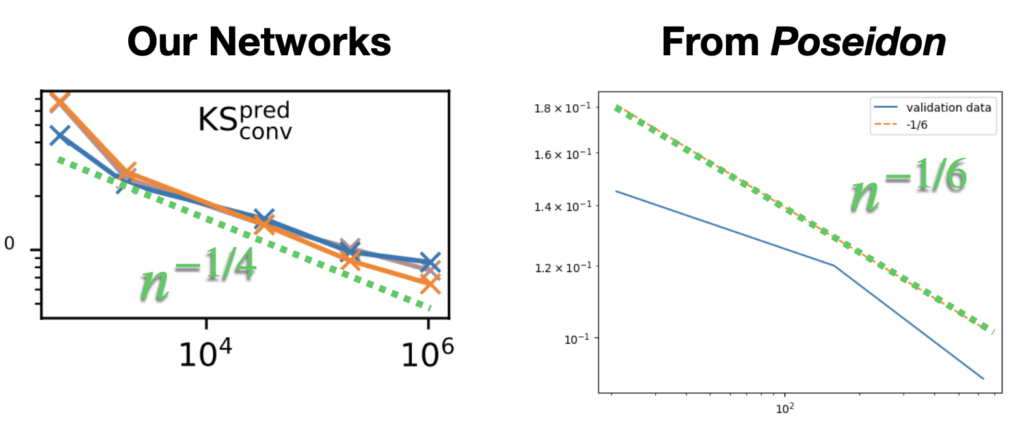
Interestingly, even for larger “foundation-model” networks there seems to be a similar scaling for the accuracy over parameters: here’s a comparison with the Poseidon paper (very interesting: https://arxiv.org/abs/2405.19101) which uses a transformer architecture , side-by-side with our experiments with a simpler ConvNet (same as above). We saw n^-1/4 , there it seems closer to n^-1/6:
Conclusions: This convergence rate is poor compared to classic numerical solvers, and indicates that neural networks are best applied for their intrinsic benefits. They possess appealing characteristics like data-driven fitting, reduced modeling biases, and flexible applications. In contrast, scaling to larger problems is more efficiently achieved by numerical approaches. In applications, it is thus advisable to combine both methods to render the benefits of both components. It also motivates the correction hybrids, where a NN supports a numerical solver. These achieve much higher accuracies, the solver can take care of the large scale generalization, and the NN can be correspondingly smaller.
For details, please check out the full paper at: https://arxiv.org/abs/2402.12971
