Our paper on learning accurate boundary conditions for cylinder wake flows with a differentiable physics NN is online now: https://arxiv.org/abs/2308.04296 , the full title being “Unsteady Cylinder Wakes from Arbitrary Bodies with Differentiable Physics-Assisted Neural Network”
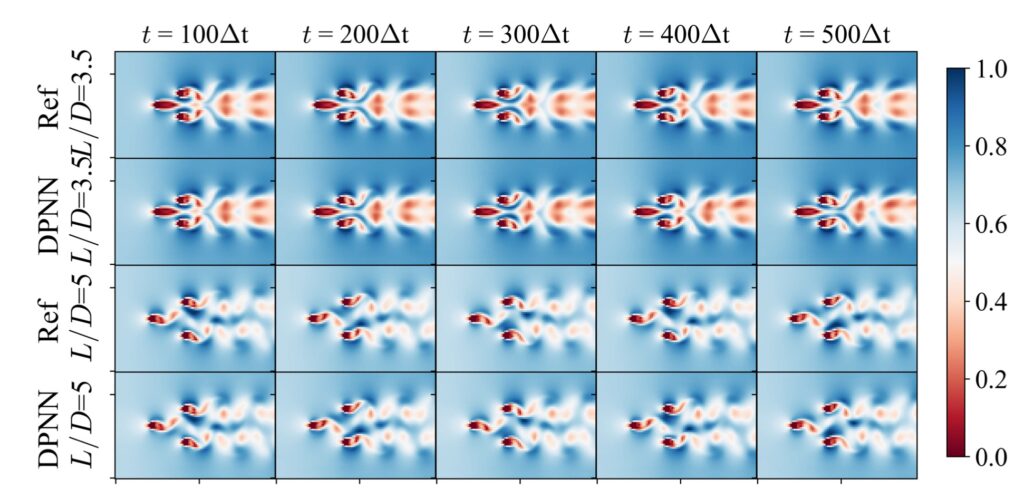
Not too surprisingly, NNs can learn very accurate boundary conditions, but the neat thing is that Shuvayan has shown they’re very useful, e.g., for studying the behavior of new arrangements of cylinders.
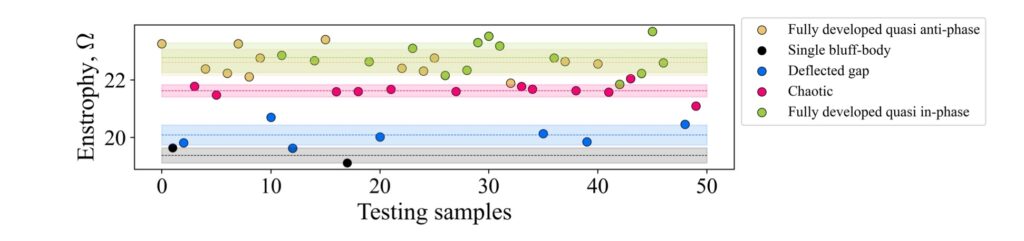
Full paper abstract: This work delineates a hybrid predictive framework configured as a coarse-grained surrogate for reconstructing unsteady fluid flows around multiple cylinders of diverse configurations. The presence of cylinders of arbitrary nature causes abrupt changes in the local flow profile while globally exhibiting a wide spectrum of dynamical wakes fluctuating in either a periodic or chaotic manner. Consequently, the focal point of the present study is to establish predictive frameworks that accurately reconstruct the overall fluid velocity flowfield such that the local boundary layer profile, as well as the wake dynamics, are both preserved for long time horizons. The hybrid framework is realized using a base differentiable flow solver combined with a neural network, yielding a differentiable physics-assisted neural network (DPNN). The framework is trained using bodies with arbitrary shapes, and then it is tested and further assessed on out-of-distribution samples. Our results indicate that the neural network acts as a forcing function to correct the local boundary layer profile while also remarkably improving the dissipative nature of the flowfields. It is found that the DPNN framework clearly outperforms the supervised learning approach while respecting the reduced feature space dynamics. The model predictions for arbitrary bodies indicate that the Strouhal number distribution with respect to spacing ratio exhibits similar patterns with existing literature. In addition, our model predictions also enable us to discover similar wake categories for flow past arbitrary bodies. For the chaotic wakes, the present approach predicts the chaotic switch in gap flows up to the mid-time range.
