We’re happy to announce that our paper titled “Score Matching via Differentiable Physics” on employing diffusion models for physical systems is available on arXiv now: https://arxiv.org/abs/2301.10250.
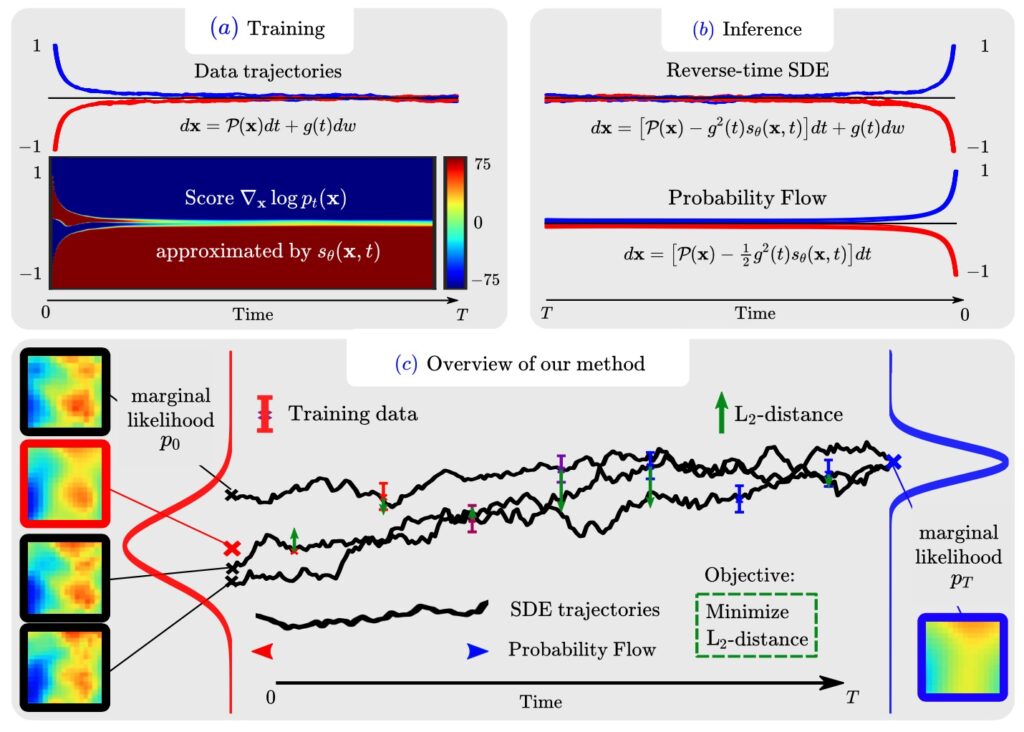
The key idea is to use a physics operator (a simulator) as “drift” term of an SDE. Among others, we give a derivation that connects the learned corrections to the score of the underlying data distribution. Here’s a visual overview:
The solutions produced by our SMDP method are (at least) on-par with regular learned methods, while providing the fundamental advantage that they allow sampling the posterior. Here’s an example from a heat equation case:

Here’s the full paper abstract:
Diffusion models based on stochastic differential equations (SDEs) gradually perturb a data distribution p(x) over time by adding noise to it. A neural network is trained to approximate the score ∇xlogpt(x) at time t, which can be used to reverse the corruption process. In this paper, we focus on learning the score field that is associated with the time evolution according to a physics operator in the presence of natural non-deterministic physical processes like diffusion. A decisive difference to previous methods is that the SDE underlying our approach transforms the state of a physical system to another state at a later time. For that purpose, we replace the drift of the underlying SDE formulation with a differentiable simulator or a neural network approximation of the physics. We propose different training strategies based on the so-called probability flow ODE to fit a training set of simulation trajectories and discuss their relation to the score matching objective. For inference, we sample plausible trajectories that evolve towards a given end state using the reverse-time SDE and demonstrate the competitiveness of our approach for different challenging inverse problems.
