Computer Graphics Forum, Volume 38 (2019) – Issue 2
Presented at Eurographics Conference 2019, May 2019

Authors
Steffen Wiewel, Technical University of Munich
Moritz Becher, Technical University of Munich
Nils Thuerey, Technical University of Munich

Abstract

We propose a method for the data-driven inference of temporal evolutions of physical functions with deep learning. More specifically, we target fluid flows, i.e. Navier-Stokes problems, and we propose a novel LSTM-based approach to predict the changes of pressure fields over time. The central challenge in this context is the high dimensionality of Eulerian space-time data sets. We demonstrate for the first time that dense 3D+time functions of physics system can be predicted within the latent spaces of neural networks, and we arrive at a neural-network based simulation algorithm with significant practical speed-ups.
We highlight the capabilities of our method with a series of complex liquid simulations, and with a set of single-phase buoyancy simulations. With a set of trained networks, our method is more than two orders of magnitudes faster than a traditional pressure solver.
Additionally, we present and discuss a series of detailed evaluations for the different components of our algorithm.

Links
Paper
Main Video
Code
Trained model
Small dataset (10 scenes with 100 frames each)
Large dataset (1000 scenes with 100 frames each)

Further Information

The variables we use to describe real world physical systems typically take the form of complex functions with high dimensionality. Especially for transient numerical simulations, we usually employ continuous models to  describe how these functions evolve over time. For such models, the field of  computational methods has been highly successful at developing  powerful numerical algorithms that accurately and efficiently predict how  the natural phenomena under consideration will behave. In the following,  we take a different view on this problem: instead of relying on analytic  expressions, we use a deep learning approach to infer physical functions based on data. More specifically, we will focus on the temporal evolution of complex functions that arise in the context of fluid flows. Fluids  encompass a large and important class of materials in human environments, and as such they’re particularly interesting candidates for learning models.
While other works have demonstrated that machine learning methods are highly competitive alternatives to traditional methods, e.g., for computing local interactions of particle based liquids, to perform divergence free projections for a single point in time, or for adversarial training of high resolution flows, few works exist that target temporal evolutions of physical systems.
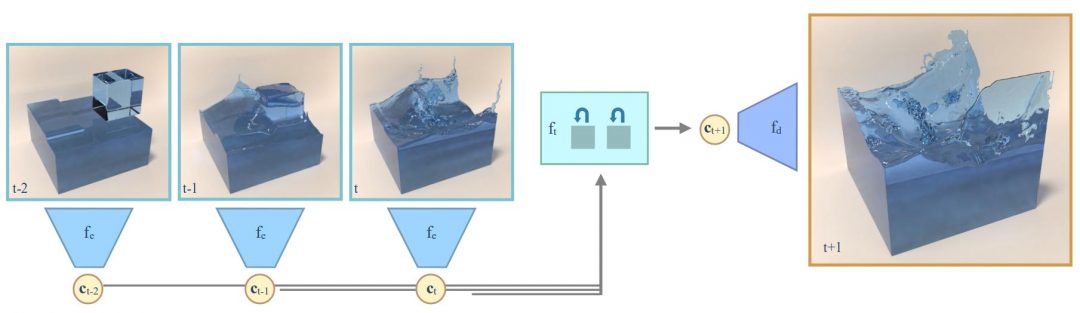
While first works have considered predictions of Lagrangian objects such  as rigid bodies, and control of two dimensional interactions, the question whether neural networks (NNs) can predict the evolution of complex three-dimensional functions such as pressure fields of fluids has not previously been addressed. We believe that this is a particularly interesting challenge, as it not only can lead to faster forward simulations, as we will demonstrate below, but also could be useful for giving NNs predictive capabilities for complex inverse problems.The complexity of nature at human scales makes it necessary to finely discretize both space and time for traditional numerical methods, in turn leading to a large number of degrees of freedom. Key to our method is reducing the dimensionality of the problem using convolutional neural networks (CNNs) with respect to both time and space. Our method first learns to map the original, three-dimensional problem into a much smaller spatial latent space, at the same time learning the inverse mapping. We then train a second network that maps a collection of reduced representations into an encoding of the temporal evolution. This reduced temporal state is then used to output a sequence of spatial latent space representations, which are decoded to yield the full spatial data set for a point in time. A key advantage of CNNs in this context is that they give us a natural way to compute accurate and highly efficient non-linear representations. We will later on demonstrate that the setup for computing this reduced representation strongly influences how well the time network can predict changes over time, and we will demonstrate the generality of our approach with several liquid and single-phase problems. The specific contributions of this work are:

  • a first LSTM architecture to predict temporal evolutions of dense, physical 3D functions in learned latent spaces,
  • an efficient encoder and decoder architecture, which by means of a strong compression, yields a very fast simulation algorithm,
  • in addition to a detailed evaluation of training modalities.
This work was funded by the ERC Starting Grant realFlow (StG-2015-637014).