Computer Graphics Forum (2018), Volume 37 (2018), Issue 8, p. 47-58
Best Paper Award from Symposium on Computer Animation (2018)

Authors
Marie-Lena Eckert, Technical University of Munich, Germany
Wolfgang Heidrich, King Abdullah University of Science and Technology, Saudi Arabia
Nils Thuerey, Technical University of Munich, Germany
Abstract
We present a novel method to reconstruct a fluid’s 3D density and motion based on just a single sequence of images. This is rendered possible by using powerful physical priors for this strongly under-determined problem. More specifically, we propose a novel strategy to infer density updates strongly coupled to previous and current estimates of the flow motion. Additionally, we employ an accurate discretization and depth-based regularizers to compute stable solutions. Using only one view for the reconstruction reduces the complexity of the capturing setup drastically and could even allow for online video databases or smart-phone videos as inputs. The reconstructed 3D velocity can then be flexibly utilized, e.g., for re-simulation, domain modification or guiding purposes. We will demonstrate the capacity of our method with a series of synthetic test cases and the reconstruction of real smoke plumes captured with a Raspberry Pi camera.
Keywords
physically-based simulation, inverse problem, fluid reconstruction, convex optimization
Links
![]() Wiley Online Library
Wiley Online Library
![]() Preprint
Preprint
![]() Video
Video
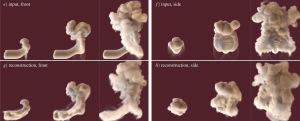
Fig. 1: Front and side views of ground truth input simulation e,f) and reconstruction g,h) of a rotationally variant jet stream. The front view (single input view) is matched very closely while the side view shows the plausible and interesting fluid motion generated by our reconstruction algorithm.
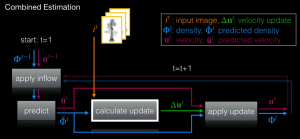
Fig. 2: Overview over our whole combined density and velocity estimation procedure including prediction, update calculation and update alignment steps.
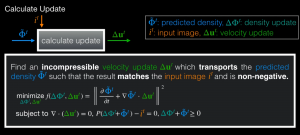
Fig. 3: Intuition and equations for our inverse problem of calculating the incompressible velocity update that leads to a realistic density distribution that matches the input image.
Further Information
While physical simulations have gained popularity in visual effects, simulations are not easy to control, especially for artists. As detailed and realistic simulations require high computational power, it is often infeasible to run multiple simulations until both the desired visuals and behavior are reached. Other approaches for creating visual effects come with their own disadvantages, e.g., compositing video data requires large collections of footage and is difficult to combine with 3D elements. Since humans are very familiar with fluid phenomena from everyday situations such as pouring milk in coffee or burning candles, the corresponding visual effects have high requirements for accuracy in order to be visually convincing.
Instead of simulating fluids purely synthetically, our goal is to reconstruct motions of real fluid phenomena in 3D such that the density matches the input image and adheres to the underlying physical models. Thus, we are solving the inverse problem to fluid simulation. Reconstructing a real fluid phenomenon directly leads to a plausible velocity field with a known visual shape, yielding an excellent starting point for, e.g., a guided simulation for visual effects. While previous fluid capture techniques typically require multiple cameras and a complex setup, we focus on reconstructions from a single camera view. This allows for the use of a large variety of existing videos and for the capture of new fluid motions with ease.
Existing computed tomography methods (e.g. [Ihrke et al. 2004]) are designed for inputs with a multitude of cameras and viewing angles. Their reconstruction quality rapidly drops with the number of views as the corresponding inverse problem becomes under-determined. Our setting of using just a single view is a challenging scenario, where we aim for plausible but not necessarily accurate reconstructions through the use of physical constraints as priors. A system with a single camera also has distinct advantages, including reduced costs, a drastically simplified setup, and the elimination of tedious procedures like camera calibration and synchronization. Without having a reliable, a-priori density reconstruction, estimating flow velocities is significantly more challenging than in previous work [Gregson et al. 2014]. Information about the motion of a fluid phenomenon allows us to flexibly re-use the captured data once it is reconstructed. It ensures temporal coherence and enables us to edit the reconstruction, to couple it with external physics solvers or to conveniently integrate the reconstructed flow in 3D environments, e.g., to render it from a new viewpoint. We will demonstrate the capabilities of our method with a variety of complex synthetic flows and with real data from a fog machine video.
In summary, our core technical contributions are
• an image formation model for the joint reconstruction of 3D densities and flow fields from single-view video sequences,
• a new optimization-based formulation of the inverse problem with a strong emphasis on temporal coherence of the recovered density sequence,
• a tailored combination of physics-based as well as geometric priors, including new priors to resolve motion uncertainty along lines of sight in the single camera view and finally
• an efficient implementation based on primal-dual optimization to realize an effective single view fluid capture system. This system is used for extensive experiments using both real and simulated data.
Real Captures and Their Reconstruction

Fig. 4: Our inexpensive and simple capturing setup for capturing smoke produced by a fog machine with a Raspberry Pi camera.
With our inexpensive and easy-to-use hardware setup of a fog machine and a Raspberri Pi camera, we recorded rising plumes of real smoke. Two of our raw input recordings are shown in Fig. 5 a) and d). We post-process these input videos with a gray-scale mapping, noise reduction and background separation. If images are captured with more complex lighting and background, we could potentially include more advanced methods from the image processing area in the post-processing step. Regarding the real capturing setup, the unknown and temporally changing smoke inflow at the bottom of the images presents an additional challenge. Therefore, we impose a velocity in the inflow region for both real reconstructions. The velocity is the same for both captures and is roughly estimated from the videos. Our algorithm still reconstructs a realistic volumetric motion that matches the input very well and produces realistic swirls from the side view. Renderings with a similar visual style but slightly different camera properties are shown below each raw input row of Fig. 5.


Fig. 5: Two captures of real fluids a,d) and reconstructions front d,e) and side views c,f). Frames are shown in 15 frame intervals.
This work is supported by the ERC Starting Grant 637014.