We are releasing our PICT solver! 🥳 it features a fully-differentiable, accurate and validated incompressible Navier-Stokes solver with seamless PyTorch integration. This enables a wide variety of neat learning tasks, such as correcting Neural operators, closure learning and inverse problems. You can find a first few examples in the accompanying paper below. Please give it a try, and let us know how it works 🤔🙏
- Source Code: https://github.com/tum-pbs/PICT
- Paper with Examples: https://arxiv.org/abs/2505.16992
- Overview Video: https://youtu.be/GGLidL0oT3s
Key results and properties of the solver are
✅ Accurate and optimized gradients
✅ Handles 2D & 3D turbulence cases
✅ Learn sub-grid scale (SGS) models from statistics alone
✅ Verified on classic benchmarks
✅ Runs faster than high-fidelty simulations — with comparable (or even better) accuracy
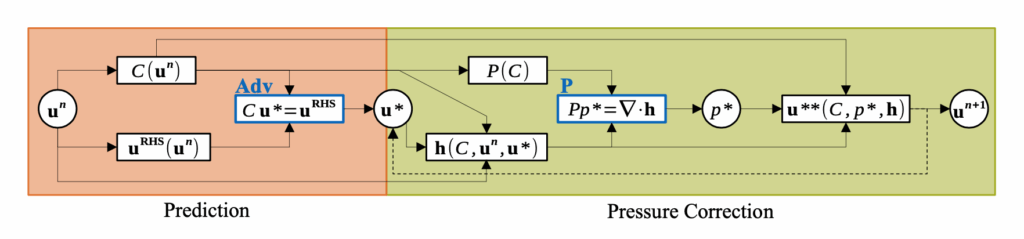
The following computational graph gives an overview of the approach. A key distinguishing feature of PICT are its tailored and efficient gradient calculations that can be leveraged to substantially accelerate back-propagation to facilitate learning tasks. E.g., the implicit derivative operators can be used deactivate parts of the backwards task in early learning stages, and enable them later on for “fine-tuning”.
Full paper abstract: Despite decades of advancements, the simulation of fluids remains one of the most challenging areas of in scientific computing. Supported by the necessity of gradient information in deep learning, differentiable simulators have emerged as an effective tool for optimization and learning in physics simulations. In this work, we present our fluid simulator PICT, a differentiable pressure-implicit solver coded in PyTorch with Graphics-processing-unit (GPU) support. We first verify the accuracy of both the forward simulation and our derived gradients in various established benchmarks like lid-driven cavities and turbulent channel flows before we show that the gradients provided by our solver can be used to learn complicated turbulence models in 2D and 3D. We apply both supervised and unsupervised training regimes using physical priors to match flow statistics. In particular, we learn a stable sub-grid scale (SGS) model for a 3D turbulent channel flow purely based on reference statistics. The low-resolution corrector trained with our solver runs substantially faster than the highly resolved references, while keeping or even surpassing their accuracy. Finally, we give additional insights into the physical interpretation of different solver gradients, and motivate a physically informed regularization technique.

