It’s worth pointing out that our paper on “How Temporal Unrolling Supports Neural Physics Simulators” is online now: https://arxiv.org/abs/2402.12971
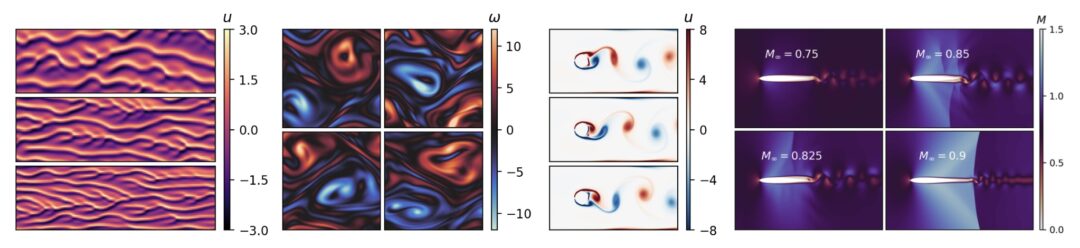
One of the key findings is: don’t throw away your simulator (yet) even if it doesn’t have gradients. You can get substantial accuracy boosts (around 5x) by coupling an NN with the simulator, instead of letting the NN do all the work… Here are results for a KS and a turbulence case:
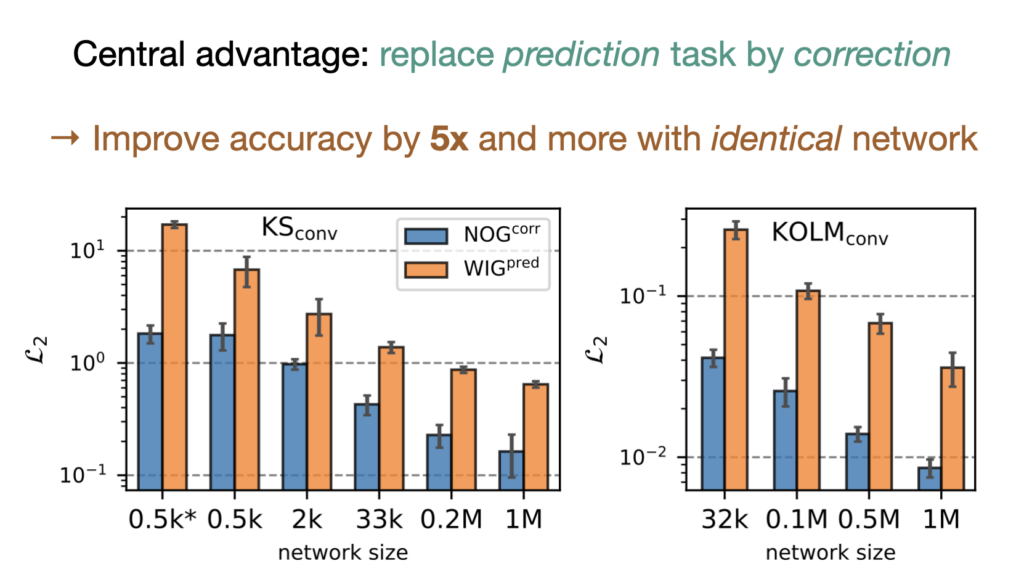
Paper Abstract: Unrolling training trajectories over time strongly influences the inference accuracy of neural network-augmented physics simulators. We analyze these effects by studying three variants of training neural networks on discrete ground truth trajectories. In addition to commonly used one-step setups and fully differentiable unrolling, we include a third, less widely used variant: unrolling without temporal gradients. Comparing networks trained with these three modalities makes it possible to disentangle the two dominant effects of unrolling, training distribution shift and long-term gradients. We present a detailed study across physical systems, network sizes, network architectures, training setups, and test scenarios. It provides an empirical basis for our main findings: A non-differentiable but unrolled training setup supported by a numerical solver can yield 4.5-fold improvements over a fully differentiable prediction setup that does not utilize this solver. We also quantify a difference in the accuracy of models trained in a fully differentiable setup compared to their non-differentiable counterparts. While differentiable setups perform best, the accuracy of unrolling without temporal gradients comes comparatively close. Furthermore, we empirically show that these behaviors are invariant to changes in the underlying physical system, the network architecture and size, and the numerical scheme. These results motivate integrating non-differentiable numerical simulators into training setups even if full differentiability is unavailable. We also observe that the convergence rate of common neural architectures is low compared to numerical algorithms. This encourages the use of hybrid approaches combining neural and numerical algorithms to utilize the benefits of both.