Congratulations to Hao, Aleksandra and Bjoern for their NeurIPS paper: https://tum-pbs.github.io/inc-paper/ 👍 It analyzes how hybrid PDE solvers fundamentally and provably benefit from “indirect” (force-based) corrections rather than direct (explicit) ones. Baking the corrections into governing equations via our method, dubbed “Indirect Neural Corrections” (INC), reduces error growth without restricting architectures or solvers. Across systems from 1D chaos to 3D turbulence, INC stabilizes rollouts, prevents blowups, and delivers very substantial speed-ups—sometimes by orders of magnitude.
The full source code is already available at: https://github.com/tum-pbs/INC/
And the arXiv preprint at: https://arxiv.org/abs/2511.12764
We believe both the theory and core approach are important steps forward for combining modern AI with classic numerical solvers, opening the door to robust scientific and engineering models at scale.
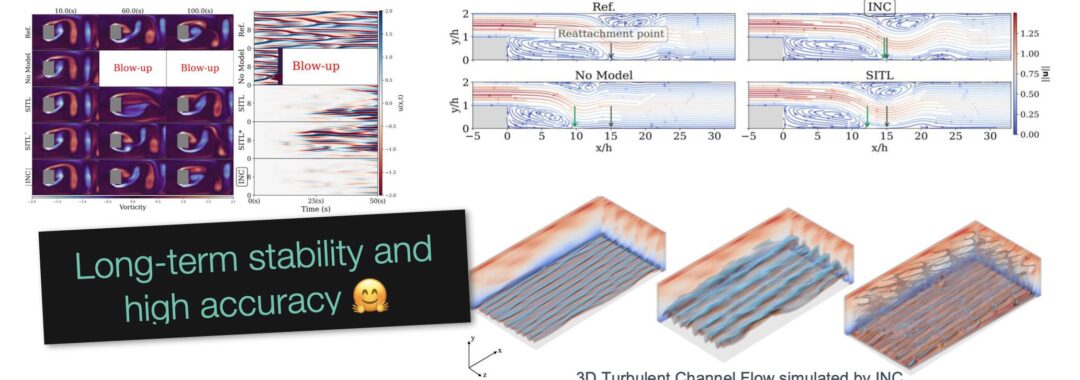
Full paper abstract: When simulating partial differential equations, hybrid solvers combine coarse numerical solvers with learned correctors. They promise accelerated simulations while adhering to physical constraints. However, as shown in our theoretical framework, directly applying learned corrections to solver outputs leads to significant autoregressive errors, which originate from amplified perturbations that accumulate during long-term rollouts, especially in chaotic regimes.
To overcome this, we propose the Indirect Neural Corrector (INC), which integrates learned corrections into the governing equations rather than applying direct state updates. Our key insight is that INC reduces the error amplification on the order of (1/dt)+L, where dt is the timestep and L the Lipschitz constant. At the same time, our framework poses no architectural requirements and integrates seamlessly with arbitrary neural networks and solvers. We test in extensive benchmarks, covering numerous differentiable solvers, neural backbones, and test cases ranging from a 1D chaotic system to 3D turbulence.
INC improves the long-term trajectory performance (R^2) by up to 158%, stabilizes blowups under aggressive coarsening, and for complex 3D turbulence cases yields speed-ups of several orders of magnitude. INC thus enables stable, efficient PDE emulation with formal error reduction, paving the way for faster scientific and engineering simulations with reliable physics guarantees.