Making a “fair” comparison between neural networks (NNs) and traditional solvers can be quite challenging and often leads to headaches 🤯. One major pitfall is comparing the NN directly with the solver used to generate the training data. In such cases, the NN will inevitably show a higher error compared to the high fidelity solver used to produce the training data. To ensure a more balanced and realistic — a “fair” — comparison, it’s essential to lower the fidelity of the solver—this gives a more accurate reflection of the NN’s performance. This is especially important when considering practical, real-world applications where we care about the accuracy produced by a chosen solver — whether it’s learned or not.
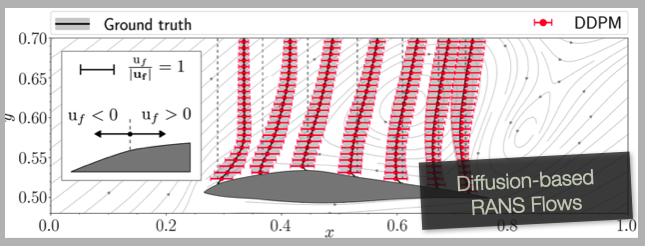
In our own work with airfoil diffusion models (https://github.com/tum-pbs/Diffusion-based-Flow-Prediction), we made finally added this more nuanced approach, adjusting the solver fidelity for a more meaningful comparison. (Shame on us that we didn’t include this in the original submission…) Even with this adjustment, we observed that the NN still delivered a 9.5x speedup on CPU compared to the classic solver (OpenFoam), and when leveraging GPU acceleration, we saw an additional order of magnitude improvement. These results highlight the significant efficiency gains achievable with neural network models, especially when accounting for the accuracy of the final output.
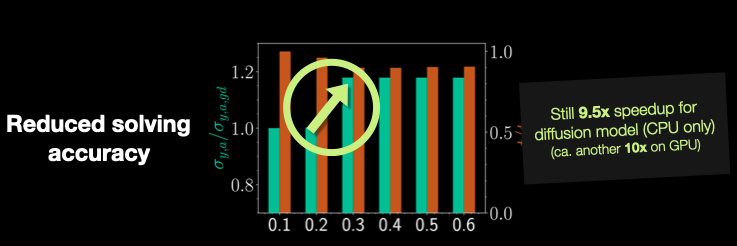
Please check out page 26 (Fig. 21) of our paper for details!