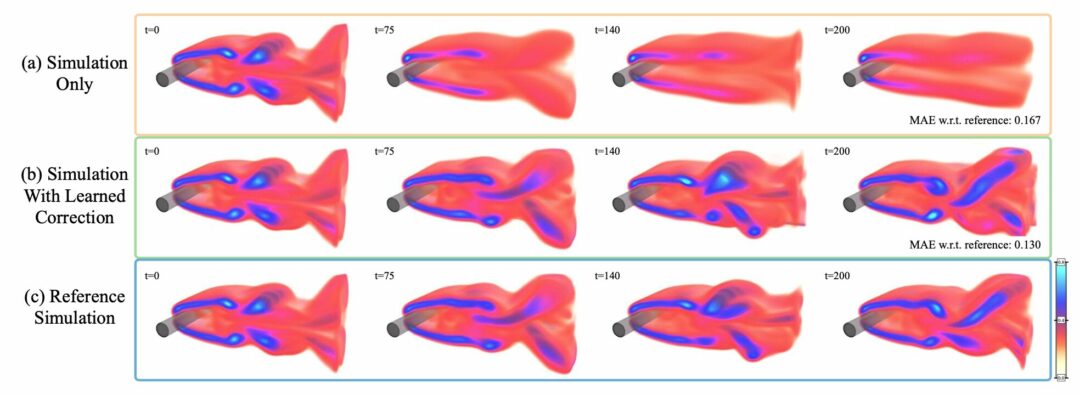
We’re happy to report that our paper on using differentiable physics to reduce errors in PDEs is online now, and a corresponding overview talk is also available now:
– Solver-in-the-Loop: Learning from Differentiable Physics to Interact with Iterative PDE-Solvers
– Differentiable Physics Simulations for Deep Learning, Talk by Nils Thuerey
Our results demonstrate that Differentiable Physics are a powerful tool, and they neatly fit into the current larger deep learning trend of generic “Differentiable Programming”. They not only yield very good minimizers in terms of well-trained neural networks: a nice side effect is that they allow for leveraging all the existing powerful numerical methods that exist for physical simulations, and employ them to improve training deep neural nets.
Solver-in-the-Loop Paper Abstract: Finding accurate solutions to partial differential equations (PDEs) is a crucial task in all scientific and engineering disciplines. It has recently been shown that machine learning methods can improve the solution accuracy by correcting for effects not captured by the discretized PDE. We target the problem of reducing numerical errors of iterative PDE solvers and compare different learning approaches for finding complex correction functions. We find that previously used learning approaches are significantly outperformed by methods that integrate the solver into the training loop and thereby allow the model to interact with the PDE during training. This provides the model with realistic input distributions that take previous corrections into account, yielding improvements in accuracy with stable rollouts of several hundred recurrent evaluation steps and surpassing even tailored supervised variants. We highlight the performance of the differentiable physics networks for a wide variety of PDEs, from non-linear advection-diffusion systems to three-dimensional Navier-Stokes flows.