Published in Neural Computing and Applications Journal
Authors: You Xie, Nils Thuerey
Abstract
The pressing need for pretraining algorithms has been diminished by numerous advances in terms of regularization, architectures, and optimizers. Despite this trend, we re-visit the classic idea of unsupervised autoencoder pretraining and propose a modified variant that relies on a full reverse pass trained in conjunction with a given training task. This yields networks that are {\em as-invertible-as-possible}, and share mutual information across all constrained layers. We additionally establish links between singular value decomposition and pretraining and show how it can be leveraged for gaining insights about the learned structures. Most importantly, we demonstrate that our approach yields an improved performance for a wide variety of relevant learning and transfer tasks ranging from fully connected networks over residual neural networks to generative adversarial networks. Our results demonstrate that unsupervised pretraining has not lost its practical relevance in today’s deep learning environment.
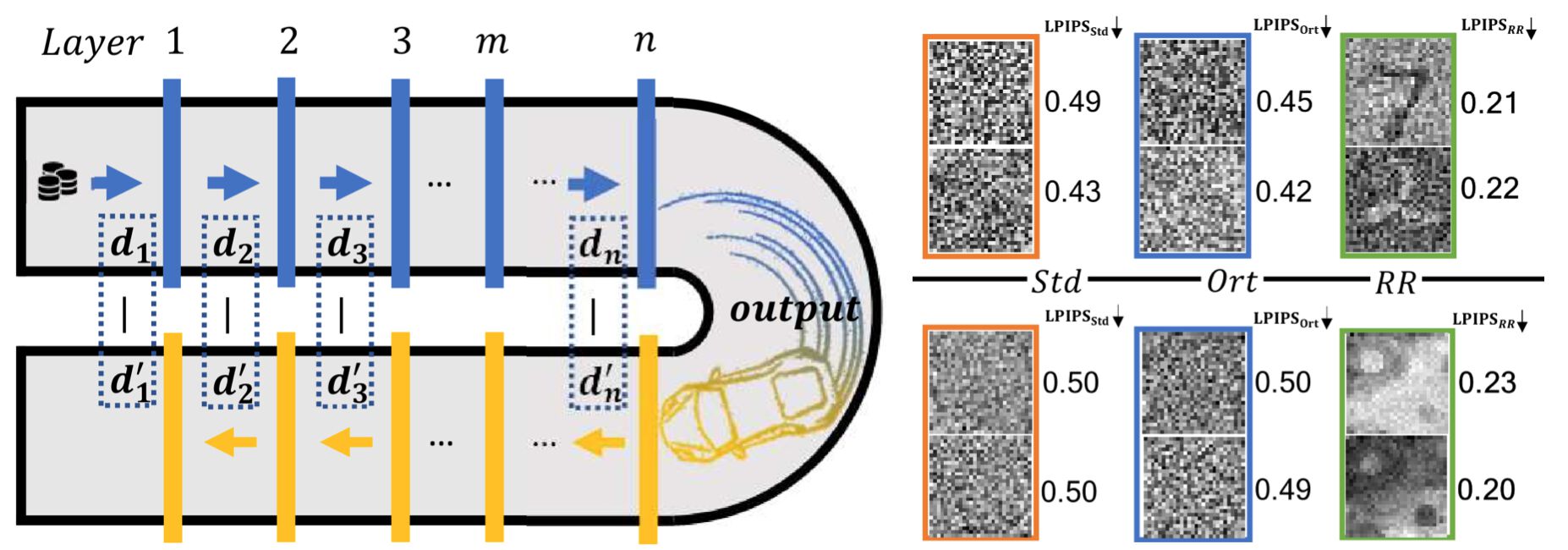
Fig. 1: We propose a novel forward-reverse network structure that re-uses all weights of a network (left), including the regular forward pass (blue) and the corresponding reverse pass (yellow). The input of layer $m$ is denoted by $d_m$. It has positive effects for learning generic features across a wide range of tasks. In addition, we demonstrate that it yields a way to embed human interpretable singular vectors into the weight metrics (right).
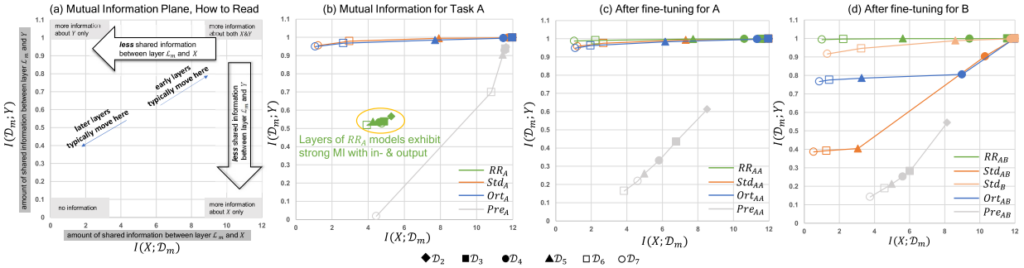
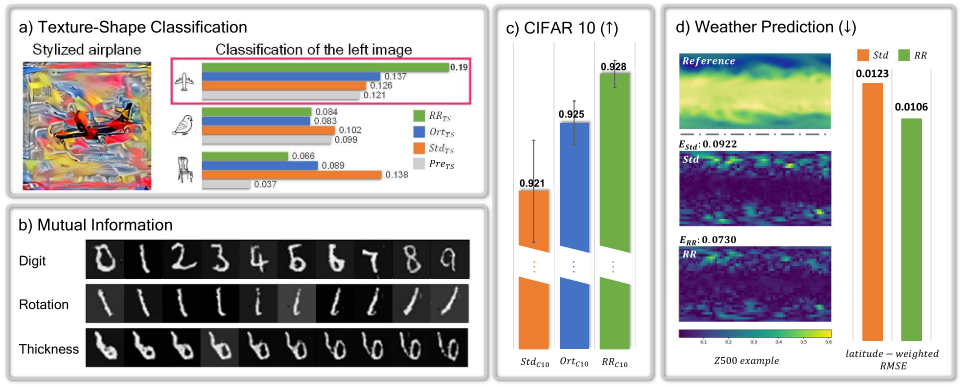
Fig. 2: Mutual Information(MI) planes for different models: a) Visual overview of the contents. b) Plane for task A. Points on each line correspond to layers of one type of model. All points of $RR_A$, are located in the center of the graph, while $Std_A$ and $Ort_A$, exhibit large $I(\data{m};Y)$, i.e., specialize on the output. $Pre_A$ strongly focuses on reconstructing the input with high $I(X; \data{m})$ for early layers. c,d) After fine-tuning for A/B. The last layer $\data{7}$ of $RR_{AA}$ and $RR_{AB}$ successfully builds the strongest relationship with $Y$, yielding the highest accuracy.

Fig. 3: MI plane comparisons among $RR_{A}^{1}$, local variant $lRR_A$ and the full version $RR_A$. Points on each line correspond to layers of one type of model. a) MI Plane for task A. All points of $RR_A$ and the majority of points for $lRR_A$ (five out seven) are located in the center of the graph, i.e., successfully connect in- and ouput distributions. b,c) After fine-tuning for A/B. The last layer $\data{7}$ of $RR_{AA/AB}$ builds the strongest relationship with $Y$. $I(\data{7};Y)$ of $lRR_{AA/AB}$ is only slightly lower than $RR_{AA/AB}$.
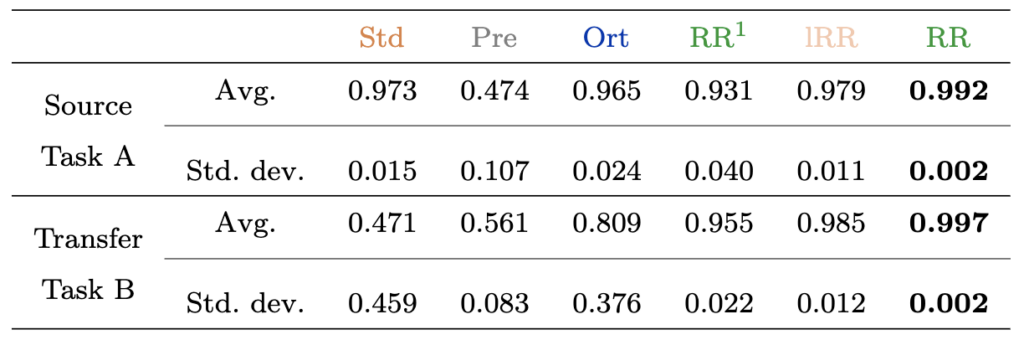
Tab. 1: Performance of MI source and transfer tasks in figure 2 and figure 3.
Application-Weather Forecasting
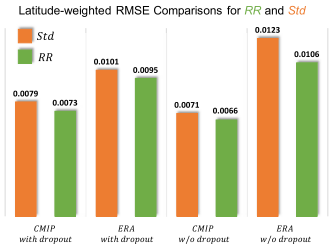
Fig.4: Latitude-weighted RMSE comparisons between Std and RR for ERA and CMIP datasets. Models trained with RR pretraining significantly outperform state-of-the-art Std for all cases. The minimum performance improvement of RR is 5.7% for the case with ERA dataset and dropout regularization.

Fig. 5: a) Comparisons of predictions for T2M and T850 on 9 Aug. 2019, 22:00 for the ERA dataset without dropout regularization. b) Prediction comparisons of three physical quantities on 26 June 2014, 0:00 for the CMIP dataset without dropout regularization. As confirmed by the quantified results, RR predicts results closer to the reference.